题目内容
19.已知平面向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,m),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则2$\overrightarrow{a}$+3$\overrightarrow{b}$=(-4,7).分析 由向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,m),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,求出m的值,则2$\overrightarrow{a}$+3$\overrightarrow{b}$的答案可求.
解答 解:∵向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,m),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴-2+2m=0,解得m=1,
则2$\overrightarrow{a}$+3$\overrightarrow{b}$=2×(1,2)+3×(-2,1)=(-4,7).
故答案为:(-4,7).
点评 本题考查了平面向量数量积的运算,考查了平面向量的坐标运算,是基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
10.设集合M={x|x∈Z且-10≤x≤-3},N={x|x∈Z且|x|≤5 },则M∪N中元素的个数为( )
| A. | 11 | B. | 10 | C. | 16 | D. | 15 |
7.某几何体的三视图如图所示,则这个几何体外接球的表面积为( )
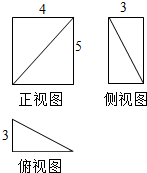

| A. | 20π | B. | 40π | C. | 50π | D. | 60π |
4.若函数$f(x)=\left\{\begin{array}{l}sinx+\frac{3}{2},x≥0\\{x^2}+a,x<0\end{array}\right.$(其中a∈R)的值域为$[\frac{1}{2},+∞)$,则a的取值范围是( )
| A. | $[\frac{3}{2},+∞)$ | B. | $[\frac{1}{2},\frac{3}{2}]$ | C. | $[\frac{1}{2},\frac{5}{2}]$ | D. | $[\frac{1}{2},+∞)$ |
9.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$,满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,且|$\overrightarrow{c}$-$\overrightarrow{a}$|+|$\overrightarrow{c}$-2$\overrightarrow{b}$|=$\sqrt{5}$,则|$\overrightarrow{c}$+2$\overrightarrow{a}$|的取值范围是( )
| A. | [1,3] | B. | [2$\sqrt{2}$,3] | C. | [$\frac{6\sqrt{5}}{5}$,2$\sqrt{2}$] | D. | [$\frac{6\sqrt{5}}{5}$,3] |
 如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.
如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.