题目内容
已知圆C: 直线
直线
(1)证明:不论 取何实数,直线
取何实数,直线 与圆C恒相交;
与圆C恒相交;
(2)求直线 被圆C所截得的弦长的最小值及此时直线
被圆C所截得的弦长的最小值及此时直线 的方程.
的方程.
【答案】
(1)见解析;(2)最短弦为4 ;直线方程为
;直线方程为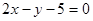
【解析】
试题分析:(1)只须确定直线上一定点在圆内,则过圆内一点的直线恒与圆相交;(2)由弦心距、半弦、半径构成的直角三角形可过A作AC的垂线,此时的直线与圆C相交于B、D两点,根据圆的几何性质可得,线段BD为直线被圆所截得最短弦,从而求出最短弦和对应的直线.
试题解析:(1)证明:直线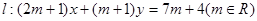 可化为:
可化为: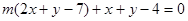 ,由此知道直线必经过直线
,由此知道直线必经过直线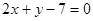 与
与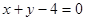 的交点,解得:
的交点,解得: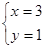 ,则两直线的交点为A(3,1),而此点在圆的内部,故不论
,则两直线的交点为A(3,1),而此点在圆的内部,故不论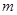 为任何实数,直线
为任何实数,直线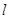 与圆C恒相交。
与圆C恒相交。
(2)联结AC,过A作AC的垂线,此时的直线与圆C相交于B、D两点,根据圆的几何性质可得,线段BD为直线被圆所截得最短弦,此时|AC|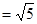 ,|BC|=5,所以|BD|=4
,|BC|=5,所以|BD|=4 。
。
即最短弦为4 ;又直线AC的斜率为
;又直线AC的斜率为 ,所求的直线方程为
,所求的直线方程为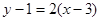 ,即
,即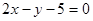
考点:1.直线与圆的位置关系;2.圆的弦长求法.

练习册系列答案
相关题目