题目内容
10.设${f_{\;}}(x)=\frac{1}{{{4^x}+2}}$,先分别求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),然后归纳猜想一般性结论,并给出证明.分析 利用条件,求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),归纳猜想一般性结论,利用指数的性质给出证明.
解答 解:f(0)+f(1)=$\frac{1}{2}$,
同理可得:f(-1)+f(2)=$\frac{1}{2}$,f(-2)+f(3)=$\frac{1}{2}$.
一般性结论:$f(x)+f(1-x)=\frac{1}{2}$或写成“若x1+x2=1,则f(x1)+f(x2)=$\frac{1}{2}$.”
证明:$f(x)+f(1-x)=\frac{1}{{{4^x}+2}}+\frac{1}{{{4^{1-x}}+2}}=\frac{1}{{{4^x}+2}}+\frac{4^x}{{{4^x}({4^{1-x}}+2)}}$=$\frac{1}{{{4^x}+2}}+\frac{4^x}{{{4^{\;}}+2×{4^x}}}=\frac{1}{{{4^x}+2}}+\frac{4^x}{{2(2+{4^x})}}$=$\frac{{2+{4^x}}}{{2(2+{4^x})}}=\frac{1}{2}$,
点评 本题考查归纳推理,考查学生分析解决问题的能力,正确归纳猜想是关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
18.椭圆16x2+25y2=400的长轴长为( )
| A. | 5 | B. | 10 | C. | 25 | D. | 50 |
5.在四面体P-ABC的四个面中,是直角三角形的面至多有( )个.
| A. | 0个 | B. | 1个 | C. | 3个 | D. | 4个 |
2.设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-2)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-2)∪(0,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-2,0)∪(2,+∞) | D. | (-2,0)∪(0,2) |
20.某校为响应市委关于创建国家森林城市的号召,决定在校内招募16名男生和14名女生作为志愿者参与相关的活动,经调查发现,招募的男女生中分别有10人和6人担任校学生干部,其余人未担任何职务.
(1)根据以上数据完成2×2列联表:
(2)根据2×2列联表的独立性检验,能否在犯错的概率不超过0.10的前提下认为性别与担任学生干部有关?
(3)如果从担任学生干部的女志愿者中(其中恰好有3人会朗诵)任意选2人在晨会上发言,则选到的志愿者中至少有一人会朗诵的概率是多少?
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
(1)根据以上数据完成2×2列联表:
职务 性别 | 担任学生干部 | 未担任学生干部 | 总计 |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
(3)如果从担任学生干部的女志愿者中(其中恰好有3人会朗诵)任意选2人在晨会上发言,则选到的志愿者中至少有一人会朗诵的概率是多少?
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
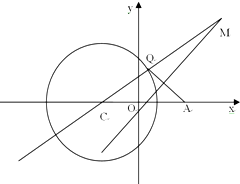 如图,已知圆$C:{(x+\sqrt{3})^2}+{y^2}=8,A(\sqrt{3},0)$,Q是圆上一动点,AQ的垂直平分线交直线CQ于点M,设点M的轨迹为E.
如图,已知圆$C:{(x+\sqrt{3})^2}+{y^2}=8,A(\sqrt{3},0)$,Q是圆上一动点,AQ的垂直平分线交直线CQ于点M,设点M的轨迹为E.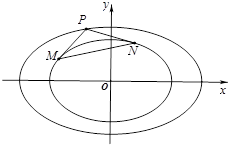 已知椭圆${C_1}:\frac{x^2}{2}+{y^2}=1$
已知椭圆${C_1}:\frac{x^2}{2}+{y^2}=1$