题目内容
已知函数 是在R上是单调递增函数,则实数a的取值范围是________.
是在R上是单调递增函数,则实数a的取值范围是________.
[7,8)
分析:由已知中函数 是在R上是单调递增函数,根据指数函数与一次函数单调性与参数的关系,我们可得一次函数的一次项系数大于0,且指数函数的底数大于1,且在x=6时,第一个解析式对应的函数值不小于第二段函数解析式对应的函数值.
是在R上是单调递增函数,根据指数函数与一次函数单调性与参数的关系,我们可得一次函数的一次项系数大于0,且指数函数的底数大于1,且在x=6时,第一个解析式对应的函数值不小于第二段函数解析式对应的函数值.
解答:若函数 是在R上是单调递增函数,
是在R上是单调递增函数,
则
解得7≤a<8
故答案为:[7,8)
点评:本题考查的知识点是函数单调性的性质,其中根据指数函数和一次函数的单调性,及分段函数单调性的性质,构造关于a的不等式组是解答本题的关键.但在解答过程中,易忽略在x=6时,第一个解析式对应的函数值不小于第二段函数解析式对应的函数值,而错解为(1,8)
分析:由已知中函数
 是在R上是单调递增函数,根据指数函数与一次函数单调性与参数的关系,我们可得一次函数的一次项系数大于0,且指数函数的底数大于1,且在x=6时,第一个解析式对应的函数值不小于第二段函数解析式对应的函数值.
是在R上是单调递增函数,根据指数函数与一次函数单调性与参数的关系,我们可得一次函数的一次项系数大于0,且指数函数的底数大于1,且在x=6时,第一个解析式对应的函数值不小于第二段函数解析式对应的函数值.解答:若函数
 是在R上是单调递增函数,
是在R上是单调递增函数,则

解得7≤a<8
故答案为:[7,8)
点评:本题考查的知识点是函数单调性的性质,其中根据指数函数和一次函数的单调性,及分段函数单调性的性质,构造关于a的不等式组是解答本题的关键.但在解答过程中,易忽略在x=6时,第一个解析式对应的函数值不小于第二段函数解析式对应的函数值,而错解为(1,8)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
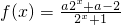 是定义在R上的奇函数.
是定义在R上的奇函数. 是定义在R上的奇函数.
是定义在R上的奇函数. 是定义在R上的单调减函数,若
是定义在R上的单调减函数,若 ,则x的范围是( )
,则x的范围是( )