题目内容
已知函数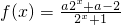 是定义在R上的奇函数.
是定义在R上的奇函数.
(1)求a的值及f(x)的解析式;
(2)判断f(x)在R上的单调性并用定义证明;
(3)求f(x)在x∈[-1,2]上的最大值及最小值.
解:(1)∵f(x)是定义在R上的奇函数
∴f(0)=0
∴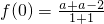
∴a=1 …(3分)
∴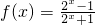 …(4分)
…(4分)
(2)f(x)在R上是增函数
证明:∵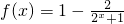
设x1<x2,则 (7分)
(7分)
∵x1<x2,∴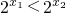
∴
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在R上是增函数. …(9分)
(3)由(2)知,f(x)在[-1,2]上是增函数 …(10分)
∴f(x)在[-1,2]上的最小值为f(-1)=- ,最大值为f(2)=
,最大值为f(2)= …(12分)
…(12分)
分析:(1)根据f(x)是定义在R上的奇函数,可得f(0)=0,代入函数中,即可求得求a的值及f(x)的解析式;
(2)先判断f(x)在R上是增函数,再用定义法证明即可;
(3)利用函数的单调性,可求f(x)在x∈[-1,2]上的最大值及最小值.
点评:本题考查函数的奇偶性,考查函数的单调性,考查函数的最值,利用定义证明函数的单调性,利用单调性求最值,是解答这道题的关键.
∴f(0)=0
∴
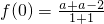
∴a=1 …(3分)
∴
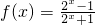 …(4分)
…(4分)(2)f(x)在R上是增函数
证明:∵
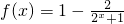
设x1<x2,则
 (7分)
(7分)∵x1<x2,∴
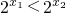
∴

∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在R上是增函数. …(9分)
(3)由(2)知,f(x)在[-1,2]上是增函数 …(10分)
∴f(x)在[-1,2]上的最小值为f(-1)=-
 ,最大值为f(2)=
,最大值为f(2)= …(12分)
…(12分)分析:(1)根据f(x)是定义在R上的奇函数,可得f(0)=0,代入函数中,即可求得求a的值及f(x)的解析式;
(2)先判断f(x)在R上是增函数,再用定义法证明即可;
(3)利用函数的单调性,可求f(x)在x∈[-1,2]上的最大值及最小值.
点评:本题考查函数的奇偶性,考查函数的单调性,考查函数的最值,利用定义证明函数的单调性,利用单调性求最值,是解答这道题的关键.

练习册系列答案
相关题目

 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时不等式
时不等式 成立, 若
成立, 若 ,
,
 ,则
,则 的大小关系是 .
的大小关系是 . 是定义在R上的增函数,且
是定义在R上的增函数,且 ,则m的取值范围是
.
,则m的取值范围是
. 是定义在R上的奇函数,
是定义在R上的奇函数, ,
,
 ,
,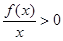 的解集是
.
的解集是
.