题目内容
若α∈（0，π）且cos（α+
）=
，则cosα=
- A.
- B.
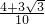
- C.
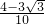
- D.
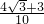
B
分析：将α表示为（α+）-，利用两角差的余弦即可求得答案．
解答：∵α∈（0，π），
∴α+∈（，
），
又cos（α+）=，
∴sin（α+）=
，
又α=（α+）-，
∴cosα=cos[（α+）-]
=cos（α+）cos+sin（α+）sin
=×
+×
=．
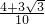故选B．
点评：本题考查两角差的余弦，将α表示为（α+）-是关键，求得sin（α+）是难点，属于中档题．
分析：将α表示为（α+
）-，利用两角差的余弦即可求得答案．解答：∵α∈（0，π），
∴α+
∈（，），又cos（α+
）=，∴sin（α+
）=，又α=（α+
）-，∴cosα=cos[（α+
）-]=cos（α+
）cos+sin（α+）sin=
×+×=
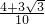．故选B．
点评：本题考查两角差的余弦，将α表示为（α+
）-是关键，求得sin（α+）是难点，属于中档题． 
练习册系列答案
相关题目
设y=f（x）是一次函数，若f（0）=1，且f（1），f（4），f（13）成等比数列，则f（2）+f（4）+…+f（2n）等于（ ）
| A、n（2n+3） | B、n（n+4） | C、2n（2n+3） | D、2n（n+4） |