Question

已知正四棱柱ABCD-A₁B₁C₁D₁中，AA₁=2AB，点E为CC₁的中点，点F为BD₁的中点．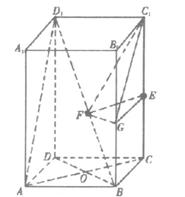

(1)求证：EF⊥平面BDD₁；

(2)求异面直线BE与C₁F所成的角；

(3)求二面角E-BB₁-F的大小．

Answer 1

解法一：(1)证明：连接AC交BD于O，∵点E为CC₁的中点，

点F肋BD₁的中点，即F为C₁A的中点

∴EF∥OC

依题意有OC⊥BD，OC⊥DD₁，故

OC⊥平面BDD₁

∴EF⊥平面BDD₁ 

(2)设G为BB₁的中点，连接FG、C₁G则召BE∥C₁G，所以∠FC₁G为异面直线BE与C₁F所成的角或补角， 

设AB=a，则在△FGC₁中，

C₁G=,FG=,FC₁=

所以C₁G²=,故cos∠FC₁G=,∴∠FC₁G=.

即异面直线BE与C₁F所成的角为. 

(3)连接EG,则由(1)知FG为EG在平面FB₁B的射影所以∠EGF为二面角E-BB₁-F的一个平面角 

在Rt△EGF为二面角E=FG,所以∠EGF=

即二面角E-BB₁-F为 

解法二:分别以DA、DC、DD₁所在的直线为x轴、y轴、z轴建立如图所示的空间直角坐标系.

设AB=1，则AA₁=2.故

B(1，1，0)，C(0，1，0)，C₁(0，1，2)，D₁(0，0，2)，E(0，1，1)，F(，，1)

(1)=(,,0)，=(0，0，2)，=(-1，-1，2)

·=×0+()×0+0×2=0

·=(-1)+()×(-1)+2×0=0

∴EF⊥DD₁，EF⊥BD₁，EF⊥平BDD₁阶段 

(2)=(-1，0，1)，(，,1)，

∴·=(-1)×()+0×+1×1=

||=，||=，

∴cos(,)=

则异面直线BE与C₁F所成的角为. 

(3)同解法一(评分同解法一).