题目内容
已知点O是原点,直线y=kx+b与圆x2+y2=
相交于两点M,N.若b2=2(k2+1),则
•
=( )
| 8 |
| 3 |
| OM |
| ON |
A、-
| ||||
B、-
| ||||
C、
| ||||
| D、0 |
分析:根据直线方程设出两点M,N的坐标,将直线方程和圆方程联立,使用根与系数的关系求出 x1+x2 和x1•x2,
代入
•
的解析式,进行计算.
代入
| OM |
| ON |
解答:解:设M(x1,kx1+b),N(x2,kx2+b),将直线方程和圆方程联立方程组并化简得
(1+k2)x2+2kbx+b2-
=0,∴x1+x2=
,x1•x2=
,
则
•
=(x1,kx1+b)•(x2,kx2+b)=x1•x2+k2x1x2+kb(x1+x2)+b2
=(1+k2)x1x2+kb(x1+x2)+b2=b2+
+kb•
+b2
=-
+
,
把b2=2(k2+1)代入式子可得
•
=
,
(1+k2)x2+2kbx+b2-
| 8 |
| 3 |
| -2kb |
| 1+k2 |
b2-
| ||
| 1+k2 |
则
| OM |
| ON |
=(1+k2)x1x2+kb(x1+x2)+b2=b2+
| -8 |
| 3 |
| -2kb |
| 1+k2 |
=-
| 8 |
| 3 |
| 2b2-2k2b2 |
| 1+k2 |
把b2=2(k2+1)代入式子可得
| OM |
| ON |
| 4 |
| 3 |
点评:本题考查一元二次方程根与系数的关系,两个向量的数量积公式的应用.

练习册系列答案
相关题目
 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点, 相交于两点M,N.若b2=2(k2+1),则
相交于两点M,N.若b2=2(k2+1),则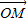
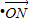 =( )
=( )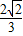


 相交于两点M,N。若b2=2(k2+1),则
相交于两点M,N。若b2=2(k2+1),则 =
=

