题目内容
本小题满分12分）
已知数列
的前n项和为
且
，
且
，数列
满足
且
．
（I）求数列的通项公式；
（II）求证：数列
为等比数列;
（III）求数列前
项和的最小值．
解： (1)由
得
, 
……2分
∴
………………4分
(2)当
时 ∵,∴
,
∴
;
又
可证
∴由上面两式得
,
∴数列是以-30为首项,
为公比的等比数列…………8分
(3)由(2)得
，∴
=
，∴是递增数列 ………10分
当n=1时, <0；当n=2时, 
<0；当n=3时, 
<0；当n=4时, 
>0，所以,从
第4项起的各项均大于0,故前3项之和最小.
且
…………………………12分
解析
练习册系列答案
相关题目
，记函数
，
的最小正周期为
. 
的值；
时，试求
上的单调递增区间．
是椭圆上纵坐标不为零的两点，若
其中F为椭圆的左焦点．
的焦点，斜率为
的直线交抛物线于
（
）两点，且
．
为坐标原点，
为抛物线上一点，若
，求
的值．
，
，
，求实数
的值;
,求实数
，且对于任意实数
，恒有
．
的解析式；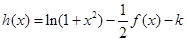
有几个零点？