Question

（本小题满分12分）

已知函数，且对于任意实数，恒有．

（1）求函数的解析式；

（2）函数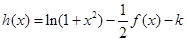有几个零点？

 

Answer 1

【答案】

（1）.

（2）时，无零点；

或时，有两个零点；

时有三个零点；

时，有四个零点.

【解析】本试题主要是考查了函数解析式的求解以及函数与方程的综合运用。

（1）根据已知中由题设得， ，则

所以 所以对于任意实数恒成立，得到b的值。

（2）令，则，然后分析函数单调性，缺的给你极值的大小进而确定零点的个数。

解：（1）由题设得，                          ……1分

，则，                          ……2分

所以 所以对于任意实数恒成立．

.                                                      ……3分

故.              ……………………………………………4分

（2）令，则.    ……6分

令，则，当变化时，的变化列表如下.

				0		1
	+	0	—	0	+	0	—
	递增	极大值	递减	极小值1	递增	极大值	递减

……9分

时，无零点；

或时，有两个零点；

时有三个零点；

时，有四个零点. ……………………………………………………12分