Question

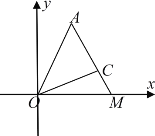
【题目】如图所示，在平面直角坐标系中，第一象限内有定点和射线，已知，的倾斜角分别为，，，， 轴上的动点与，共线．

（1）求点坐标（用表示）；

（2）求面积关于的表达式；

（3）求面积的最小时直线的方程．

Answer 1

【答案】（1）；（2）；（3）见解析

【解析】

（1）由题易知，可得C点坐标；

（2）由题易知直线, 设，共线,即斜率相等，可得，再利用面积公式求得结果；

（3）由（2）易知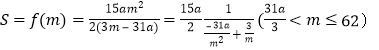，将分母看做关于的二次函数，求最值即可得出结果.

(1) ，又

(2)直线,设共线,∴

解得:,∴

(3)法一、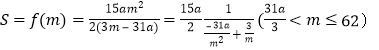

记

(ⅰ)若即,函数在上递减，当且仅当即时

取得最小值,此时,直线的方程为:

(ⅱ)若即,函数在上递增，上递减，当且仅当即时取得最小值,此时,直线的方程为:

法二、记,

以下用单调性的定义证明“对勾”函数的单调性（略）

(ⅰ)若,,在上递减,当且仅当

即时取得最小值,此时,直线的方程为:

(ⅱ)若,,在上递减, 在上递增,

当且仅当即时取得最小值,此时,直线的方程为: （法二中“对勾”函数的单调性未证明的不扣分）