题目内容
已知 ,
, ,若同时满足条件:
,若同时满足条件:
① ,
, 或
或 ,②
,②
则m的取值范围是
【答案】
(-4,0)
【解析】根据 可解得x<1,由于题目中第一个条件的限制,导致f(x)在
可解得x<1,由于题目中第一个条件的限制,导致f(x)在 是必须是
是必须是 ,当m=0时,
,当m=0时, 不能做到f(x)在
不能做到f(x)在 时
时 ,所以舍掉,因此,f(x)作为二次函数开口只能向下,故m<0,且此时2个根为
,所以舍掉,因此,f(x)作为二次函数开口只能向下,故m<0,且此时2个根为 ,为保证条件成立,只需
,为保证条件成立,只需
 ,和大前提m<0取交集结果为
,和大前提m<0取交集结果为 ;又由于条件2的限制,可分析得出在
;又由于条件2的限制,可分析得出在 恒负,因此就需要在这个范围内g(x)有得正数的可能,即-4应该比
恒负,因此就需要在这个范围内g(x)有得正数的可能,即-4应该比 两个根中较小的来的大,当
两个根中较小的来的大,当 时,
时, ,解得交集为空,舍。当m=-1时,两个根同为
,解得交集为空,舍。当m=-1时,两个根同为 ,舍。当
,舍。当 时,
时, ,解得
,解得 ,综上所述,
,综上所述, 。
。
【考点定位】本题考查学生函数的综合能力,涉及到二次函数的图像开口,根大小,涉及到指数函数的单调性,还涉及到简易逻辑中的“或”,还考查了分类讨论思想。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知椭圆 ,抛物线
,抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为坐标原点
的顶点均为坐标原点 ,从每条曲线上各取两个点,将其坐标记录于表中:
,从每条曲线上各取两个点,将其坐标记录于表中:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求 的标准方程;
的标准方程;
(2)请问是否存在直线 同时满足条件:(ⅰ)过
同时满足条件:(ⅰ)过 的焦点
的焦点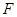 ;(ⅱ)与
;(ⅱ)与 交于不同两点
交于不同两点 、
、 ,且满足
,且满足 .若存在,求出直线
.若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.










 ,直线
,直线 和直线
和直线 ,且
,且 与
与 的距离是
的距离是
 的值
的值 ,使得
,使得 ,③
,③ 的距离之比是
的距离之比是 ,若能,求点
,若能,求点