题目内容
1.有下列命题:①$y=cos(x-\frac{π}{4})cos(x+\frac{π}{4})$的图象关于直线x=$\frac{π}{2}$对称;
②y=$\frac{x+3}{x-1}$的图象关于点(-1,1)对称;
③关于x的方程ax2-2ax-1=0有且仅有一个实根,则a=-1;
④满足条件AC=$\sqrt{3}$,∠B=60°,AB=1的三角形△ABC有两个.
其中真命题的序号是①③.
分析 利用积化和差公式化简函数解析式,进而分析其对称性,可判断①;求出函数的对称中心,可判断②;根据一元二次方程根的个数与系数的有关系,求出a值,可判断③;利用正弦定理,判断三角形解的个数,可判断④.
解答 解:①$y=cos(x-\frac{π}{4})cos(x+\frac{π}{4})$=$\frac{1}{2}${$cos[(x-\frac{π}{4})+(x+\frac{π}{4})]$+$cos[(x-\frac{π}{4})-(x+\frac{π}{4})]$}=$\frac{1}{2}$cos2x,
当x=$\frac{π}{2}$时,y取最小值,故函数图象关于直线x=$\frac{π}{2}$对称,故①正确;
函数y=$\frac{x+3}{x-1}$=$\frac{4}{x-1}$+1的图象由函数y=$\frac{4}{x}$的图象向右平移一个单位,再向上平移一个单位得到,
函数y=$\frac{4}{x}$的图关于点(0,0)对称,故函数y=$\frac{x+3}{x-1}$的图象关于点(1,1)对称,故②错误;
关于x的方程ax2-2ax-1=0有且仅有一个实根,则$\left\{\begin{array}{l}△=4{a}^{2}+4a=0\\ a≠0\end{array}\right.$,即a=-1,故③正确;
满足条件AC=$\sqrt{3}$,∠B=60°,AB=1的三角形△ABC有且只有一个,故④错误;
故正确的命题的序号为:①③,
故答案为:①③
点评 本题以命题的真假判断与应用为载体,考查了函数的对称性,函数图象的平移变换,正弦定理,积化和差公式,难度中档.

练习册系列答案
相关题目
12.下列函数中,既是定义域上的奇函数又在区间(0,1)内单调递增的是( )
| A. | $y=x+\frac{1}{x}$ | B. | y=xsinx+cosx | C. | $y={e^x}-\frac{1}{e^x}$ | D. | $y=ln\frac{1-x}{1+x}$ |
6.设全集U=R,集合M={x2+2x-3≤0},N={x|-1≤x≤4},则M∩N等于( )
| A. | {x|1≤x≤4} | B. | {x|-1≤x≤3} | C. | {x|-3≤x≤4} | D. | {x|-1≤x≤1} |
10.执行如图所示的程序框图,若x=4,则输出的y=( )


| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
11.已知函数f(x)=log${\;}_{\frac{1}{2}}$(x+1),若f(a)=3,则a的值为( )
| A. | -$\frac{3}{4}$ | B. | 7 | C. | -$\frac{7}{8}$ | D. | $\frac{7}{8}$ |
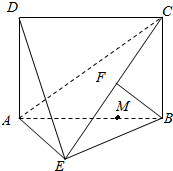 如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.
如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.