题目内容
设F1,F2为椭圆C1: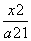 +
+ =1(a1>b1>0)与双曲线C2的公共的左、右焦点,它们在第一象限内交于点M,△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2.若椭圆C1的离心率e∈
=1(a1>b1>0)与双曲线C2的公共的左、右焦点,它们在第一象限内交于点M,△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2.若椭圆C1的离心率e∈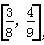 ,则双曲线C2的离心率的取值范围是( )
,则双曲线C2的离心率的取值范围是( )
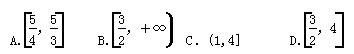
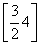
D
[解析] 设双曲线C2的方程为 -
- =1(a2>0,b2>0),由已知|MF1|=2,|F1F2|=|MF2|=2c,又根据椭圆与双曲线的定义得到:
=1(a2>0,b2>0),由已知|MF1|=2,|F1F2|=|MF2|=2c,又根据椭圆与双曲线的定义得到:
 ⇒a1-a2=2c,其中2a1、2a2分别为椭圆的长轴长和双曲线的实轴长,∵椭圆的离心率e∈
⇒a1-a2=2c,其中2a1、2a2分别为椭圆的长轴长和双曲线的实轴长,∵椭圆的离心率e∈ ,∴
,∴ ≤
≤ ≤
≤ ,
,
∴ c≤a1≤
c≤a1≤ c,而a2=a1-2c,∴
c,而a2=a1-2c,∴ c≤a2≤
c≤a2≤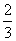 c,
c,
∴ ≤
≤ ≤4,故选D.
≤4,故选D.

练习册系列答案
相关题目
 .
.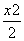 +y2=1的左焦点,点P为椭圆C上任意一点,点Q的坐标为(4,3),则|PQ|+|PF|取最大值时,点P的坐标为________.
+y2=1的左焦点,点P为椭圆C上任意一点,点Q的坐标为(4,3),则|PQ|+|PF|取最大值时,点P的坐标为________.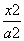 +
+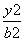 =1(a>b>0)上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cos α=
=1(a>b>0)上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cos α=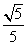 ,sin(α+β)=
,sin(α+β)=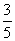 ,则此椭圆的离心率为________.
,则此椭圆的离心率为________.

 dx=3+ln 2(a>1),则a的值为( )
dx=3+ln 2(a>1),则a的值为( ) 的公差为2,若
的公差为2,若 ,
, ,
, 成等比数列,则
成等比数列,则 的前n项和
的前n项和 ( )
( ) B、
B、 C、
C、
 D、
D、