题目内容
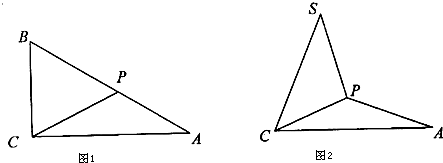
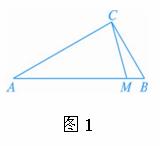
如图1所示,Rt△ABC中,BC=2,CA=3,点P在线段AB上,将△BPC沿CP折成直二面角S-CP-A(点B与点S重合),且SA=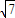 (图2).
(图2).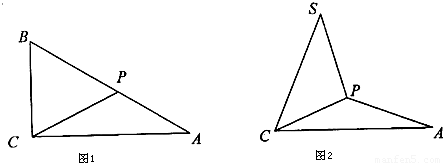
(1)求∠SCP的度数;
(2)求二面角P-SC-A的余弦值.
【答案】分析:(1)建立空间直角坐标系,用坐标表示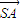 ,利用SA=
,利用SA= ,即可求得∠SCP的度数;
,即可求得∠SCP的度数;
(2)平面PSC的法向量为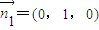 ,平面ASC的法向量为
,平面ASC的法向量为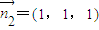 ,利用向量的夹角公式,即可求得二面角P-SC-A的余弦值.
,利用向量的夹角公式,即可求得二面角P-SC-A的余弦值.
解答:解:(1)建立如图所示的空间直角坐标系,设∠SCP=α,则A(2cosα-3sinα,3cosα,-2sinα),C(2cosα,0,0),S(0,0,2sinα)
∴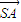 =(2cosα-3sinα,3cosα,-2sinα),
=(2cosα-3sinα,3cosα,-2sinα),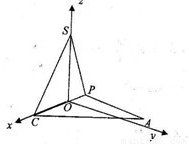
∴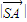 =
=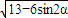 =
=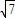 ,∴sin2α=1,∴α=
,∴sin2α=1,∴α=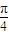
(2)平面PSC的法向量为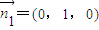
设平面ASC的法向量为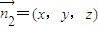
∵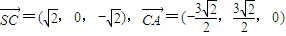
∴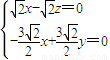 ,∴取
,∴取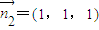
∴cos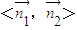 =
= =
=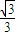
∴二面角P-SC-A的余弦值为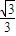 .
.
点评:本题考查利用空间向量解决立体几何问题,考查面面角,正确求出平面的法向量是关键.
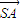 ,利用SA=
,利用SA= ,即可求得∠SCP的度数;
,即可求得∠SCP的度数;(2)平面PSC的法向量为
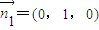 ,平面ASC的法向量为
,平面ASC的法向量为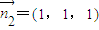 ,利用向量的夹角公式,即可求得二面角P-SC-A的余弦值.
,利用向量的夹角公式,即可求得二面角P-SC-A的余弦值.解答:解:(1)建立如图所示的空间直角坐标系,设∠SCP=α,则A(2cosα-3sinα,3cosα,-2sinα),C(2cosα,0,0),S(0,0,2sinα)
∴
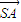 =(2cosα-3sinα,3cosα,-2sinα),
=(2cosα-3sinα,3cosα,-2sinα),
∴
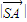 =
=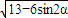 =
=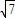 ,∴sin2α=1,∴α=
,∴sin2α=1,∴α=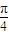
(2)平面PSC的法向量为
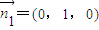
设平面ASC的法向量为
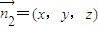
∵
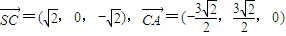
∴
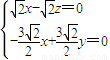 ,∴取
,∴取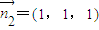
∴cos
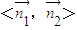 =
= =
=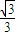
∴二面角P-SC-A的余弦值为
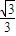 .
.点评:本题考查利用空间向量解决立体几何问题,考查面面角,正确求出平面的法向量是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
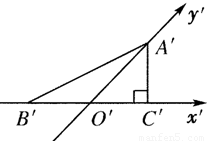
 如图所示,Rt△A′B′C′为水平放置的△ABC的直观图,其中A′C′⊥B′C′,B′O′=O′C′=1,则△ABC的面积为
如图所示,Rt△A′B′C′为水平放置的△ABC的直观图,其中A′C′⊥B′C′,B′O′=O′C′=1,则△ABC的面积为