Question

（2012•浙江模拟）如图1所示，Rt△ABC中，BC=2，CA=3，点P在线段AB上，将△BPC沿CP折成直二面角S-CP-A（点B与点S重合），且SA=

7

（图2）．

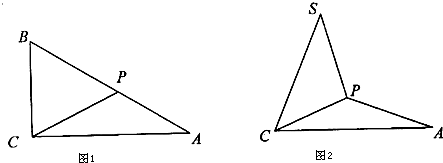
（1）求∠SCP的度数；
（2）求二面角P-SC-A的余弦值．

Answer 1

分析：（1）建立空间直角坐标系，用坐标表示

SA

，利用SA=

7

，即可求得∠SCP的度数；
（2）平面PSC的法向量为

n1

=(0，1，0)，平面ASC的法向量为

n2

=(1，1，1)，利用向量的夹角公式，即可求得二面角P-SC-A的余弦值．

解答：解：（1）建立如图所示的空间直角坐标系，设∠SCP=α，则A（2cosα-3sinα，3cosα，-2sinα），C（2cosα，0，0），S（0，0，2sinα）
∴

SA

=（2cosα-3sinα，3cosα，-2sinα），
∴|

SA

|=

13-6sin2α

=

7

，∴sin2α=1，∴α=

π

4

（2）平面PSC的法向量为

n1

=(0，1，0)
设平面ASC的法向量为

n2

=(x，y，z)
∵

SC

=(

2

，0，-

2

)，

CA

=(-

3 2

2

，

3 2

2

，0)
∴

2 x- 2 z=0 - 3 2 2 x+ 3 2 2 y=0

，∴取

n2

=(1，1，1)
∴cos＜

n1

，

n2

＞=

1

3

=

3

3

∴二面角P-SC-A的余弦值为

3

3

．

点评：本题考查利用空间向量解决立体几何问题，考查面面角，正确求出平面的法向量是关键．