题目内容
如图,三棱柱 的所有棱长都为2,
的所有棱长都为2,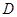 为
为 中点,
中点, 平面
平面

(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)求点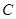 到平面
到平面 的距离.
的距离.
 的所有棱长都为2,
的所有棱长都为2,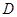 为
为 中点,
中点, 平面
平面

(1)求证:
 平面
平面 ;
;(2)求二面角
 的余弦值;
的余弦值;(3)求点
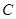 到平面
到平面 的距离.
的距离.(1)
 (2)
(2)
试题分析:(1)取
 中点
中点 ,连结
,连结 .
.  为正三角形,
为正三角形, .
. 在正三棱柱
在正三棱柱 中, 平面
中, 平面 平面
平面 ,
, 平面
平面 .
.取
 中点
中点 ,以
,以 为原点,
为原点, ,
, ,
, 的方向为
的方向为 轴的正方向建立直角坐标系,则
轴的正方向建立直角坐标系,则 ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, .
. ,
, ,
, ,
, .
.  平面
平面 .
.(2)设平面
 的法向量为
的法向量为 .
. ,
, .
. ,
, ,
,


令
 得
得
由(1)知
 平面
平面 ,
, 为平面
为平面 的法向量.
的法向量.
 二面角
二面角 的余弦值为
的余弦值为 .
.(3)由(2),
 为平面
为平面 法向量,
法向量,  .
. 点
点 到平面
到平面 的距离
的距离 .
.点评:解决的关键是能合理的建立坐标系,结合点的坐标,得到向量的坐标,从而得到法向量的坐标,借助于向量的数量积来求解,属于基础题。

练习册系列答案
相关题目
 ,直线
,直线 ,直线
,直线 ,有下面四个命题:
,有下面四个命题:  ∥
∥

 (2)
(2) 
 ∥
∥
 ∥
∥

 边长为
边长为 ,角
,角 ,沿
,沿 将
将 折起,使二面角
折起,使二面角 为
为 ,则折起后
,则折起后 、
、 之间的距离是 .
之间的距离是 . 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, .
.

 ;
; ,求二面角
,求二面角 的余弦值.
的余弦值. ,
, ,
,
 是直线,
是直线, 是平面,给出下列命题:
是平面,给出下列命题: ,
, ,
, ,则
,则 或
或 .
. ,
, ,
, ,则
,则 .
.
 ,n
,n ,n∥
,n∥ 且
且 ,
, ,则
,则
 的底面边长为4,高为3,在正三棱锥内任取一点
的底面边长为4,高为3,在正三棱锥内任取一点 ,使得
,使得 的概率是( )
的概率是( )


