题目内容
为使抛物线y=x2上的点P与A（0，-4）和B（2，0）构成的△PAB的面积最小，那么点P的坐标应为 ．
分析：先求出直线AB的方程，设直线y=2x+t是抛物线的切线，欲使得△PAB的面积最小，只须点P到直线AB的距离最小即可，直线与抛物线方程联立消去y，再根据判别式等于0求得t，代入方程求得x，进而求得y，答案可得．
解答：解：∵A（0，-4）和B（2，0）
∴直线AB的方程y=2x-4，
设直线y=2x+t是抛物线的切线，△PAB高的最小值是两直线之间的距离，
代入化简得x2-2x-t=0
由△=0得t=-1
代入方程得x=1，y=1
∴P为（1，1）
故答案为（1，1）
∴直线AB的方程y=2x-4，
设直线y=2x+t是抛物线的切线，△PAB高的最小值是两直线之间的距离，
代入化简得x2-2x-t=0
由△=0得t=-1
代入方程得x=1，y=1
∴P为（1，1）
故答案为（1，1）
点评：本题主要考查抛物线的应用和抛物线与直线的关系．考查了学生综合分析和解决问题的能力．
练习册系列答案
相关题目
x2上的点，过点Bn（n，bn）作抛物线y=
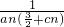}的前n项和为Sn，求证：
≤Sn＜
．
x2上的点，过点Bn（n，bn）作抛物线y=
x2的切线交x轴于点An（an，0），点Cn（cn，0）在x轴上，且点An，Bn，Cn构成以点Bn为顶点的等腰三角形．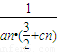
}的前n项和为Sn，求证：
≤Sn＜
．