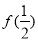题目内容
下列函数中,既是奇函数又是增函数的为( )
A. B.
B. C.
C.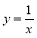 D.
D.

【解析】
试题分析:选项A:定义域为 因为
因为 所以
所以 不是奇函数;
不是奇函数;
因为当 时,
时, 所以
所以 是
是 上增函数
上增函数
综上 是
是 上增函数但不是奇函数,不选A.
上增函数但不是奇函数,不选A.
选项B:定义域为 因为
因为 所以
所以 是奇函数;
是奇函数;
因为当 时,
时, 所以
所以 是
是 上减函数,不是增函数,
上减函数,不是增函数,
综上 是奇函数但不是增函数,不选B
是奇函数但不是增函数,不选B
选项C: 定义域 ,所以单调性需在
,所以单调性需在 和
和 分别讨论,也就是说在定义域
分别讨论,也就是说在定义域 无单调性. 当
无单调性. 当 时,
时, 所以
所以 在
在 上是减函数,同理可得
上是减函数,同理可得 在
在 上也是减函数,但不能说
上也是减函数,但不能说 在定义域
在定义域 上是减函数,这是易错点;
上是减函数,这是易错点;
因为 ,定义域又关于原点对称,所以
,定义域又关于原点对称,所以 是奇函数,
是奇函数,
综上 是奇函数但不是增函数,不选C
是奇函数但不是增函数,不选C
选项D:定义域为 因为
因为 ,所以
,所以 是奇函数;
是奇函数;
因为当 时,
时, 有三种情况,一是
有三种情况,一是 ,此时
,此时 二是
二是 ,此时
,此时 三是
三是 ,此时
,此时 因此当
因此当 时,总有
时,总有 ,所以
,所以 是
是 上增函数,
上增函数,
综上 是奇函数也是增函数,选D
是奇函数也是增函数,选D
考点:奇偶性及增减性的判定

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目