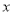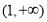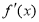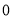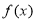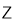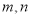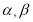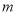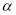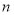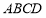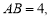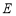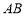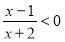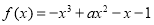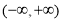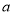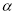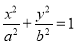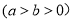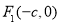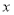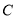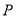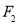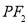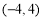题目内容
已知三次函数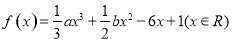 ,
,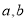 为实常数。
为实常数。
(1)若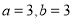 时,求函数
时,求函数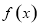 的极大、极小值;
的极大、极小值;
(2)设函数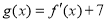 ,其中
,其中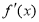 是
是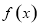 的导函数,若
的导函数,若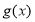 的导函数为
的导函数为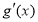 ,
,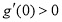 ,
,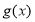 与
与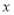 轴有且仅有一个公共点,求
轴有且仅有一个公共点,求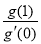 的最小值.
的最小值.
(1)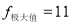 ,
,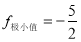 ;(2)2.
;(2)2.
【解析】
试题分析:(1)当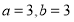 时,得到
时,得到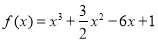 ,求其导函数,列表得到函数的单调区间,进而可得函数的极值;(2)由函数
,求其导函数,列表得到函数的单调区间,进而可得函数的极值;(2)由函数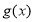 求导,得到
求导,得到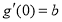 ,
,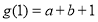 ,再由
,再由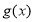 与
与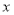 轴有且仅有一个公共点,得到
轴有且仅有一个公共点,得到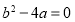 ,利用基本不等式,即可得到
,利用基本不等式,即可得到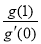 的最小值.
的最小值.
试题解析:(1)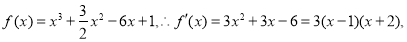
令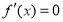 ,
,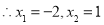 ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
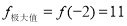 ,
,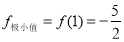 .
.
(2)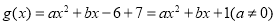 ,
,
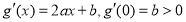 ,
,
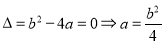 .
.
法一: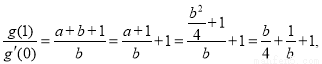 令
令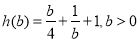 ,
,
 令
令
又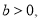 则
则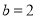 ,
,
当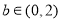 时,
时,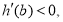
当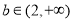 时,
时,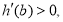
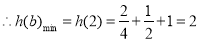 ,
,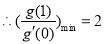 .
.
法二: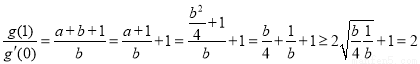 ,
,
“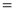 ”
”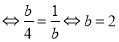 ,
,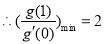 .
.
考点:1、利用导数研究极值;2、基本不等式的应用.

练习册系列答案
相关题目