题目内容
已知双曲线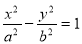 的离心率为
的离心率为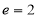 ,右焦点
,右焦点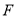 到其渐进线的距离为
到其渐进线的距离为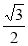 ,抛物线
,抛物线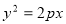 的焦点与双曲线的右焦点
的焦点与双曲线的右焦点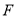 重合.过该抛物线的焦点的一条直线交抛物线于A、B两点,正三角形ABC的顶点C在直线
重合.过该抛物线的焦点的一条直线交抛物线于A、B两点,正三角形ABC的顶点C在直线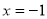 上,则△ABC的边长是 ( )
上,则△ABC的边长是 ( )
A.8 B.10 C.12 D.14
C
【解析】
试题分析:因为双曲线 的离心率
的离心率 ,所以,
,所以, ,
,
因为双曲线右焦点 到其渐进线的距离为
到其渐进线的距离为 ,所以,
,所以,

即:
双曲线的右焦点也即抛物线的焦点为F(1,0),
所以抛物线的方程为 ,
,
设AB的中点为M,过A、B、M分别作AA1、BB1、MN垂直于
直线 于A1、B1、N,设∠AFx=
于A1、B1、N,设∠AFx= ,由抛物线定义知:
,由抛物线定义知:
|MN| ,∵|MC|
,∵|MC| ,
,
∴|MN| |MC|,∵∠CMN=
|MC|,∵∠CMN= ,
,
∴ ,即
,即 ,
,
又由抛物线定义知|AF| ,|BF|
,|BF| ,∴|AB|
,∴|AB| .
.
即正三角形ABC的边长为12.故选C.
考点:1、双曲线的标准方程与简单几何性质;2、直线与抛物线的位置关系.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 的方程为
的方程为 ,则点
,则点 到直线
到直线 的距离为 .
的距离为 . .甲、乙、丙三位同学每人购买了一袋该食品。
.甲、乙、丙三位同学每人购买了一袋该食品。 的图象在点(1,f(1))处的切线方程是
的图象在点(1,f(1))处的切线方程是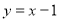 ,函数g(x)=
,函数g(x)= 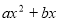 (a、b∈R,a≠0)在x=2处取得极值-2.
(a、b∈R,a≠0)在x=2处取得极值-2. (其中
(其中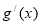 是g(x)的导函数)在区间(
是g(x)的导函数)在区间( ,
,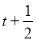 )没有单调性,求实数
)没有单调性,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式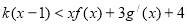 恒成立,求k的最大值.
恒成立,求k的最大值. 在
在 处取得极值0,则
处取得极值0,则 = .
= . 中,已知首项
中,已知首项 ,公差
,公差 .若
.若 ,则
,则 的最大值为 .
的最大值为 . 的两条直角边
的两条直角边 的长分别为
的长分别为 ,
, ,以
,以 为直径的圆与
为直径的圆与 交于点
交于点 则
则
 .
. 

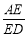 的值;若不存在,说明理由.
的值;若不存在,说明理由.