题目内容
已知函数 在
在 处取得极值0,则
处取得极值0,则 = .
= .
11
【解析】
试题分析:由 ,得:
,得:
因为函数 在
在 处取得极值0,
处取得极值0,
所以,
 ,解得:
,解得: 或
或
当 时,
时,
所以函数在R上为单调递增函数,与在在 处取得极值0相矛盾,所以
处取得极值0相矛盾,所以 不合题意,舍去;
不合题意,舍去;
当 时,
时,
所以, ,且当
,且当 时,
时, ,函数
,函数 在区间
在区间 上为减函数,
上为减函数,
当 时,
时, ,函数
,函数 在区间
在区间 上为增函数,
上为增函数,
所以函数 在
在 处取得极值.所以符合题意.所以
处取得极值.所以符合题意.所以 ,所以答案应填:11.
,所以答案应填:11.
考点:1、导数的几何意义;2、导数在研究函数性质中的应用.

练习册系列答案
相关题目
 中,
中, ,
, ,
, .
. 是等差数列,并求
是等差数列,并求 的前
的前 项和为
项和为 ,证明:
,证明: .
. ,集合
,集合 ,则集合
,则集合 ( )
( ) B.
B. C.
C. D.
D.
 (其中
(其中 >0)的图像向右平移
>0)的图像向右平移 个单位长度,所得图像经过点(
个单位长度,所得图像经过点( ,0),则
,0),则 B.1 C.
B.1 C. D.2
D.2 (
( ).
). 在[0,
在[0, ]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
]上有两个不同的零点x1、x2,求tan(x1+x2)的值.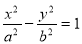 的离心率为
的离心率为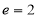 ,右焦点
,右焦点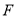 到其渐进线的距离为
到其渐进线的距离为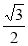 ,抛物线
,抛物线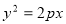 的焦点与双曲线的右焦点
的焦点与双曲线的右焦点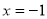 上,则△ABC的边长是 ( )
上,则△ABC的边长是 ( ) B.
B. 是
是 的充分条件
的充分条件 ,
, D.
D.  的充要条件是
的充要条件是
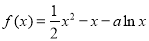 ,
,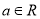 .
.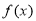 在区间
在区间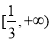 上单调递增,求
上单调递增,求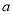 的取值范围;
的取值范围;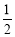 ∈A, -
∈A, -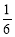 A.
A.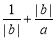 的最小值
的最小值