题目内容
(本小题满分12分)如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.

(1)求三棱锥P—ACD的外接球的表面积;
(2)若M为PB的中点,问在AD上是否存在一点E,使AM∥平面PCE?若存在,求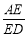 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1)5π;(2)在AD上存在点E,使AM∥平面BCE, 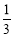 .
.
【解析】
试题分析:(1)在△ACD中,AC= ,CD=
,CD= ,AD=2,
,AD=2,
利用AC2+CD2=AD2证得AC⊥CD,根据PA⊥平面ABCD得到PA⊥CD,从而有CD⊥平面PAC, CD⊥PC;
根据△PAD、△PCD均是以PD为斜边的直角三角形,
取PD的中点O,则OA=OP=OC=OD=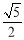 ,计算即得所求.
,计算即得所求.
(2)根据观察分析,取PC的中点N,连接MN,EN,得到MN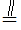
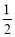 BC, 又BC∥AE,得到MN∥AE;
BC, 又BC∥AE,得到MN∥AE;
由AM∥平面PCE,得 AM∥EN,四边形AMNE为平行四边形,AE=MN=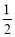 BC=
BC= AD,
AD,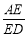 =
=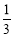 .
.
考点:1.球的表面积;2.平行关系、垂直关系.

练习册系列答案
相关题目
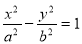 的离心率为
的离心率为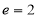 ,右焦点
,右焦点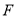 到其渐进线的距离为
到其渐进线的距离为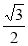 ,抛物线
,抛物线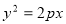 的焦点与双曲线的右焦点
的焦点与双曲线的右焦点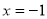 上,则△ABC的边长是 ( )
上,则△ABC的边长是 ( )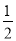 ,则C的方程是( ).
,则C的方程是( ).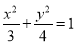 B、
B、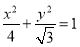 C、
C、 D、
D、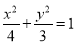
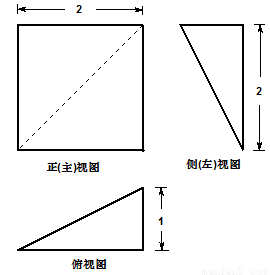
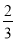 B.
B.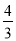 C.
C. D.
D.
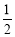 ∈A, -
∈A, -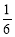 A.
A.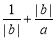 的最小值
的最小值 (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))= , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .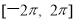 内随机取两个数分别记为
内随机取两个数分别记为 则使得函数
则使得函数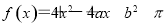 有零点的概率为( )
有零点的概率为( ) B.
B. C.
C. D.
D.
 满足
满足 ,
, (
( ),则
),则 的值为 .
的值为 .  在
在 上有意义,则实数
上有意义,则实数 的取值范围为
的取值范围为 B.
B.  C.
C.  D.
D. 