Question

10．圆心为O，半径为4的圆上两弦AB与CD垂直相交于点P，且|PO|=2，则|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$+$\overrightarrow{PD}$|=4．

Answer 1

分析 如图所示，过点O分别作OM⊥AB，ON⊥CD，垂足分别M，N，根据垂经定理可得：M，N分别为弦AB，CD的中点．于是$\overrightarrow{PA}+\overrightarrow{PB}$=$\overrightarrow{PM}+\overrightarrow{MA}+\overrightarrow{PB}$=$\overrightarrow{PM}+\overrightarrow{BP}+\overrightarrow{PM}+\overrightarrow{PB}$=2$\overrightarrow{PM}$．同理可得：$\overrightarrow{PC}+\overrightarrow{PD}$=2$\overrightarrow{PN}$，代入即可得出．

解答 解：如图所示，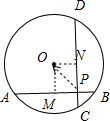
过点O分别作OM⊥AB，ON⊥CD，垂足分别M，N，则M，N分别为弦AB，CD的中点．
则$\overrightarrow{PA}+\overrightarrow{PB}$=$\overrightarrow{PM}+\overrightarrow{MA}+\overrightarrow{PB}$=$\overrightarrow{PM}+\overrightarrow{BP}+\overrightarrow{PM}+\overrightarrow{PB}$=2$\overrightarrow{PM}$．
同理可得：$\overrightarrow{PC}+\overrightarrow{PD}$=2$\overrightarrow{PN}$，
∴|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$+$\overrightarrow{PD}$|=|2$\overrightarrow{PM}+2\overrightarrow{PN}$|=2$|\overrightarrow{PO}|$=4．
故答案为：4．

点评 本题考查了向量的平行四边形法则、向量共线定理、向量的模，考查了推理能力与计算能力，属于中档题．