题目内容
2.廉华超市每月按出厂价3元/瓶购进一种饮料,根据以前的统计数据,若零售价定为4元/瓶,每月可销售400瓶;每瓶售价每降低0.05元,则可多销售40瓶,在每个月的进货量当月售完的前提下,请你给该超市设计一个方案:售价应定为多少元和从工厂购进多少瓶时,才可获得最大利润.分析 先设销售价为x元/瓶,则由题意知当月销售量进而得出当月销售所得的利润,再根据二次函数的性质求得f(x)取得最大值扩这时进货量即得答案.
解答 解:设销售价为x元/瓶,则由题意知当月销售量为:
$\frac{4-x}{0.05}$×40+400=400(9-2x)(瓶)(3分)
故当月销售所得的利润为:
f(x)=400(9-2x)(x-3)=400(-2x2+15x-27)(元)(6分)
根据二次函数的性质知,当x=$\frac{15}{4}$=3.75(元)时,
f(x)取得最大值450(元).(9分)
这时进货量应为400(9-2x)=400(9-2×$\frac{15}{4}$)=600(瓶).(11分)
所以,当销售价定为每瓶3.75元和每月购进600瓶该种饮料时,
可获得最大利润450元.(12分)
点评 本题主要考查函数模型的选择与应用、二次函数的性质等,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.

练习册系列答案
相关题目
12.对于大于1的自然数m的三次幂可用奇数进行以下方式的“分裂”:23=3+5,33=7+9+11,43=13+15+17+19,…,仿此,若m3的“分裂数”中有一个是61,则m的值是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
11.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是( )
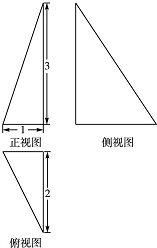

| A. | 1 m3 | B. | 2 cm3 | C. | 3 cm3 | D. | 6 cm3 |
12.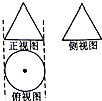 一个几何体的三视图如图所示,其中正视图和侧视图都是边长为2的正三角形,那么这个几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图都是边长为2的正三角形,那么这个几何体的体积为( )
 一个几何体的三视图如图所示,其中正视图和侧视图都是边长为2的正三角形,那么这个几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图都是边长为2的正三角形,那么这个几何体的体积为( )| A. | $\frac{\sqrt{3}}{3}π$ | B. | $\frac{\sqrt{2}}{2}π$ | C. | $\frac{\sqrt{2}}{4}π$ | D. | $\frac{π}{4}$ |