题目内容
已知抛物线x2=-12y的切线l垂直于直线x+y=0,则l的方程为____________.
解析:设切线为l:y=x+b,代入抛物线方程得x2+12x+12b=0.
由Δ=144-36b=0,得b=3.
故切线l的方程为y=x+3.
答案:y=x+3

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知抛物线x2=4y的焦点F和点A(-1,8),P为抛物线上一点,则|PA|+|PF|的最小值是( )
| A、16 | B、12 | C、9 | D、6 |
已知抛物线x2=4
y的准线过双曲线
-y2=-1的一个焦点,则双曲线的离心率为( )
| 3 |
| x2 |
| m2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2
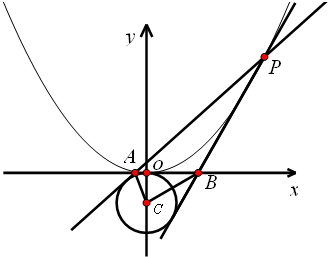
已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2 已知抛物线x2=4y的焦点为F,过F任作直线l(l与x轴不平行)交抛物线分别于A,B两点,点A关于y轴对称点为C,
已知抛物线x2=4y的焦点为F,过F任作直线l(l与x轴不平行)交抛物线分别于A,B两点,点A关于y轴对称点为C,