Question

已知抛物线x²=2py（p＞0）．抛物线上的点M（m，1）到焦点的距离为2
（1）求抛物线的方程和m的值；
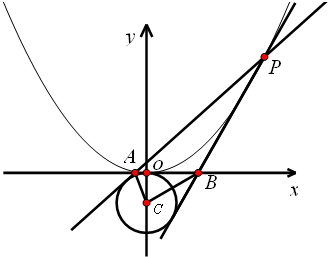
（2）如图，P是抛物线上的一点，过P作圆C：x²+（y+1）²=1的两条切线交x轴于A，B两点，若△CAB的面积为

3 3

5

，求点P坐标．

Answer 1

分析：（Ⅰ）由抛物线定义易得 1+

p

2

=2，解得p．即可得到抛物线方程，把（m，1）代入抛物线方程即可得到m．
（II）当切线PB或PA斜率不存在，不符合题意．当切线PA，PB斜率都存在．即t≠±1，设切线方程为：y-

t2

4

=k(x-t)，利用圆心C（0，-1）到切线距离为半径1和点到直线的距离公式可得 

|1+ t2 4 -kt|

k2+1

=1，化为关于k的一元二次方程，得到根与系数的关系．利用切线PA：y-

t2

4

=k1(x-t)，切线PB：y-

t2

4

=k2(x-t)，可得点A，B的坐标，再利用S_△ABC=

1

2

|AB|×1即可得出．

解答：解：（Ⅰ）由抛物线定义易得 1+

p

2

=2，解得p=2．
∴抛物线方程为x²=4y，
把（m，1）代入抛物线方程得m²=4，
解得m=±2．
（2）设点P(t，

t2

4

)，当切线PB斜率不存在，P(1，

1

4

)，设切线PA：y-

1

4

=k0(x-1)，
圆心C（0，-1）到切线距离为半径1，

|1+ 1 4 -k0|

k 2 0 +1

=1，解得k₀=

9

40

，
∴A(-

1

9

，0)，∴S△ABC=

5

9

，不符合题意．
同理当切线PA斜率不存在，S△ABC=

5

9

，不符合题意．
当切线PA，PB斜率都存在．即t≠±1，
设切线方程为：y-

t2

4

=k(x-t) 圆心C（0，-1）到切线距离为半径1，即 

|1+ t2 4 -kt|

k2+1

=1，
两边平方整理得：(t2-1)k2-2t(1+

t2

4

)k+

t4

16

+

t2

2

=0，设k₁，k₂为方程的两根．
 韦达定理得：

△= t4 4 +6t2＞0 k1+k2= 2t(1+ t2 4 ) (t2-1) k1k2= t4 16 + t2 2 (t2-1)

，
则切线PA：y-

t2

4

=k1(x-t)，切线PB：y-

t2

4

=k2(x-t)，得A(

-t2

4k1

+t，0)，B(

-t2

4k2

+t，0)，
S_△ABC=

1

2

|AB|×1=

1

2

×

t2

4

×|

1

k1

-

1

k2

|
=

t2

8

|

k1-k2

k1k2

|=

t2

8

•

(k1+k2)2-4k1k2

|k1k2|

=

t2

8

•

t4 4 +6t2

|t2-1|

•

|t2-1|

t4 16 + t2 2

=

t4+24t2

t2+8

=

3 3

5

，
化为（t²-12）（t²-72）=0，解得t²=12或72．
∴t=±2

3

，±6

2

．∴P(±2

3

，3)，P(±6

2

，18)．

点评：本题考查了抛物线的定义及其标准方程、圆的切线的性质、点到直线的距离公式、三角形的面积公式、弦长公式、分类讨论等基础知识与基本技能方法，属于难题．