题目内容
如图, 、
、 、…、
、…、
 是曲线
是曲线 :
: 上的
上的 个点,点
个点,点 (
( )在
)在 轴的正半轴上,且
轴的正半轴上,且 是正三角形(
是正三角形( 是坐标原点).
是坐标原点).
(1)写出 、
、 、
、 ;
;
(2)求出点 (
( )的横坐标
)的横坐标 关于
关于 的表达式并证明.
的表达式并证明.
 、
、 、…、
、…、
 是曲线
是曲线 :
: 上的
上的 个点,点
个点,点 (
( )在
)在 轴的正半轴上,且
轴的正半轴上,且 是正三角形(
是正三角形( 是坐标原点).
是坐标原点).(1)写出
 、
、 、
、 ;
;(2)求出点
 (
( )的横坐标
)的横坐标 关于
关于 的表达式并证明.
的表达式并证明.
(Ⅰ)
(2) .
.

(2)
 .
.(1)依题意,得 .解得
.解得 ;
;
 .解得
.解得 ;同理
;同理 .(2)由
.(2)由 猜想
猜想 .利用数学归纳法证明,
.利用数学归纳法证明, 时,
时, 成立;假定当
成立;假定当 时命题成立,即有
时命题成立,即有 ,寻找
,寻找 与
与 的关系,用
的关系,用 去证明.根据已知得
去证明.根据已知得 ,及
,及 ,得
,得 ,即
,即 .把
.把 代入求
代入求 ,保证
,保证 .即得证明
.即得证明
(Ⅰ)
(2)依题意,得 ,由此及
,由此及 得
得
 ,即
,即 .
.
由(Ⅰ)可猜想: .
.
下面用数学归纳法予以证明:(1)当 时,命题显然成立;
时,命题显然成立;
(2)假定当 时命题成立,即有
时命题成立,即有 ,则当
,则当 时,由归纳假设及
时,由归纳假设及
 得
得 ,即
,即
 ,
,
解之得: (
( 不合题意,舍去),
不合题意,舍去),
即当 时,命题成立.
时,命题成立.
由(1)、(2)知:命题成立
 .解得
.解得 ;
;
 .解得
.解得 ;同理
;同理 .(2)由
.(2)由 猜想
猜想 .利用数学归纳法证明,
.利用数学归纳法证明, 时,
时, 成立;假定当
成立;假定当 时命题成立,即有
时命题成立,即有 ,寻找
,寻找 与
与 的关系,用
的关系,用 去证明.根据已知得
去证明.根据已知得 ,及
,及 ,得
,得 ,即
,即 .把
.把 代入求
代入求 ,保证
,保证 .即得证明
.即得证明(Ⅰ)

(2)依题意,得
 ,由此及
,由此及 得
得 ,即
,即 .
.由(Ⅰ)可猜想:
 .
.下面用数学归纳法予以证明:(1)当
 时,命题显然成立;
时,命题显然成立;(2)假定当
 时命题成立,即有
时命题成立,即有 ,则当
,则当 时,由归纳假设及
时,由归纳假设及 得
得 ,即
,即 ,
,解之得:
 (
( 不合题意,舍去),
不合题意,舍去),即当
 时,命题成立.
时,命题成立.由(1)、(2)知:命题成立

练习册系列答案
相关题目
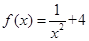 (x≠0),各项均为正数的数列
(x≠0),各项均为正数的数列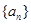 中
中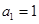 ,
,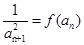 ,
,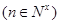 .
.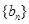 中,对任意的正整数
中,对任意的正整数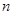 ,
, 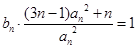 都成立,设
都成立,设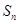 为数列
为数列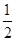 的大小.
的大小. 是一个等差数列,且
是一个等差数列,且

 , 以及Sn的最大值.
, 以及Sn的最大值.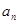 }的前n项和为
}的前n项和为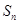 ,已知
,已知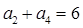 ,
,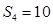 .
.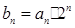
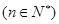 ,求数列{
,求数列{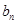 }的前项和
}的前项和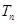 .
. (n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且
(n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且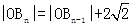 (n=2,3,4,…).
(n=2,3,4,…). ;
; 面积的最大值.
面积的最大值.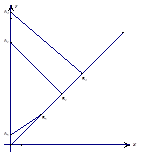
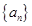 的前n项和为
的前n项和为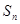 ,首项
,首项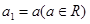 ,公差
,公差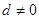 ,且
,且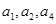 成等比数列。
成等比数列。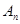 =
=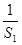 +
+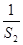 +
+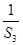 +…+
+…+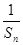 ,
, 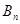 =
=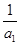 +
+ 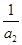 +
+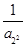 +… +
+… +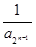 ,
,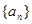 满足a1=1,且
满足a1=1,且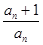 =
=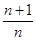 ,则
,则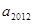 =( )
=( )