题目内容
已知函数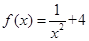 (x≠0),各项均为正数的数列
(x≠0),各项均为正数的数列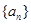 中
中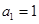 ,
,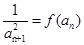 ,
,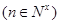 .
.
(Ⅰ)求数列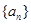 的通项公式;
的通项公式;
(Ⅱ)在数列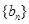 中,对任意的正整数
中,对任意的正整数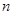 ,
, 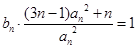 都成立,设
都成立,设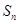 为数列
为数列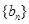 的前
的前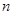 项和试比较
项和试比较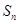 与
与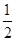 的大小.
的大小.
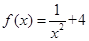 (x≠0),各项均为正数的数列
(x≠0),各项均为正数的数列 中
中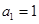 ,
,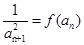 ,
,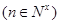 .
.(Ⅰ)求数列
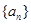 的通项公式;
的通项公式;(Ⅱ)在数列
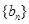 中,对任意的正整数
中,对任意的正整数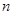 ,
, 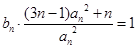 都成立,设
都成立,设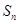 为数列
为数列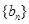 的前
的前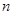 项和试比较
项和试比较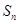 与
与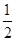 的大小.
的大小.(1)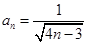 ;
;
(2)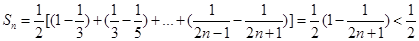
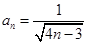 ;
;(2)
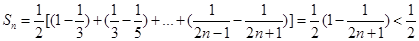
(I) 解题的关键是由题意知 ,
,
∴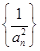 是以1为首项4为公差的等差数列.
是以1为首项4为公差的等差数列.
(II)先确定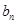
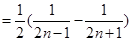 ,然后采用裂项求和的方法求和即可.
,然后采用裂项求和的方法求和即可.
解:(Ⅰ)由题意知 ,
,
∴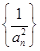 是以1为首项4为公差的等差数列 .
是以1为首项4为公差的等差数列 .
∴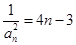 , ∴
, ∴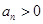 , ∴
, ∴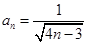 . ...................6分
. ...................6分
(Ⅱ)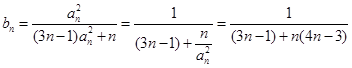
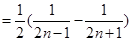 ,
,
∴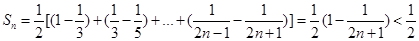 .
.
...................13分
 ,
,∴
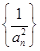 是以1为首项4为公差的等差数列.
是以1为首项4为公差的等差数列.(II)先确定
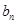
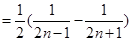 ,然后采用裂项求和的方法求和即可.
,然后采用裂项求和的方法求和即可.解:(Ⅰ)由题意知
 ,
,∴
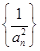 是以1为首项4为公差的等差数列 .
是以1为首项4为公差的等差数列 .∴
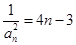 , ∴
, ∴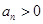 , ∴
, ∴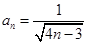 . ...................6分
. ...................6分(Ⅱ)
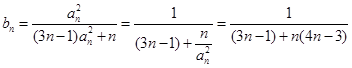
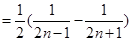 ,
,∴
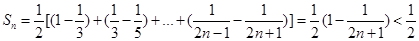 .
....................13分

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
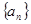 满足
满足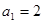 ,
,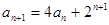
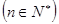 .
. 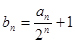 ,求证:数列
,求证:数列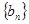 为等比数列;
为等比数列;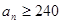 的最小正整数
的最小正整数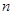 .
.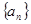 和
和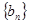 的前
的前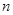 项和为
项和为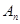 和
和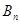 ,且
,且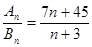 ,则
,则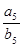 为( )
为( )
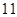

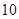
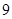
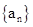 的前n项和
的前n项和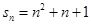 ;
;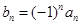 (n∈N*);则数列
(n∈N*);则数列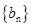 的前50项和为 ( )
的前50项和为 ( )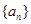 是等差数列,首项
是等差数列,首项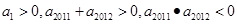 ,则使前n项和
,则使前n项和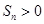 成立的最大自然数n是( )
成立的最大自然数n是( ) ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式.
,求Tn的表达式. 、
、 、…、
、…、
 是曲线
是曲线 :
: 上的
上的 个点,点
个点,点 (
( )在
)在 轴的正半轴上,且
轴的正半轴上,且 是正三角形(
是正三角形( 是坐标原点).
是坐标原点). 、
、 、
、 ;
; (
( )的横坐标
)的横坐标 关于
关于
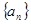 (
(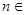 N+)中,
N+)中,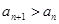 ,
,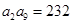 ,
,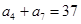 .
. 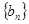 ,具体方法如下:
,具体方法如下: 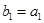 ,
,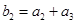 ,
,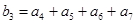 ,
,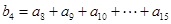 ,…,依此类推,
,…,依此类推,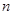 项
项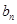 由相应的
由相应的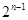 项的和组成,求数列
项的和组成,求数列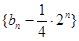 的前
的前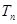 .
.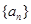 的前
的前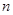 项和
项和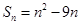 ,第
,第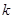 项满足
项满足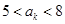 ,则
,则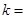 ( )
( )