题目内容
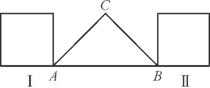
如图,在△ABC中,∠C=90°,AC=BC=2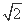 ,一个边长2的正方形由位置Ⅰ沿边AB平行移动到位置Ⅱ,若移动的距离为x,正方形和三角形的公共部分的面积为f(x).
,一个边长2的正方形由位置Ⅰ沿边AB平行移动到位置Ⅱ,若移动的距离为x,正方形和三角形的公共部分的面积为f(x).
(1) 求f(x)的解析式;
(2) 在坐标系中画出函数y=f(x)的草图;
(3) 根据图象,指出函数y=f(x)的单调区间和最大值.

(1) 由题设,当0≤x≤2时,f(x)= x·x=
x·x= x2;
x2;
当2<x<4时,f(x)= ·2
·2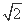 ·2
·2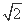 -
- (x-2)·(x-2)-
(x-2)·(x-2)- ·(4-x)·(4-x)=-(x-3)2+3;
·(4-x)·(4-x)=-(x-3)2+3;
当4≤x≤6时,f(x)= (6-x)·(6-x)=
(6-x)·(6-x)= (x-6)2.
(x-6)2.
所以f(x)=
(2) 函数f(x)的图象如下:

(第9题)
(3) 由图象观察知,函数f(x)的单调增区间为[0,3],单调减区间为[3,6],
当x=3时,函数f(x)取最大值为3.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 ,+∞) B.(1,+∞)
,+∞) B.(1,+∞)
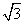 sin
sin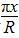 图象上相邻的一个最大值点与一个最小值点恰好都在圆x2+y2=R2上,则f(x)的最小正周期为( )
图象上相邻的一个最大值点与一个最小值点恰好都在圆x2+y2=R2上,则f(x)的最小正周期为( )