题目内容
E是二面角α---l---β的棱上一点，EF?β，EF与l成45°角，与α成30°角，则该二面角的大小为（ ）
分析：利用线面垂直的判定和性质定理作出二面角的平面角，进而利用含30°、45°角的直角三角形的边角关系及其正弦函数即可求出．
解答：解：如图所示，过点F作FO⊥α，垂足为O，连接OE，则∠OEF即为直线与平面α所成的角，
再过点O作OP⊥l交l于点P，连接FP，根据三垂线定理可得l⊥OF，∴∠OPF即为二面角α---l---β的平面角．
不妨设OF=1，在Rt△OFE中，∠OEF=30°，∴EF=2，OE=
．
在等腰Rt△PEF中，∠PEF=45°．∴PE=PF=
．
在Rt△OPF中，sin∠OPF=
=
=
，∴∠OPF=45°．
∴二面角α---l---β的平面角为45°．
故选A．
再过点O作OP⊥l交l于点P，连接FP，根据三垂线定理可得l⊥OF，∴∠OPF即为二面角α---l---β的平面角．
不妨设OF=1，在Rt△OFE中，∠OEF=30°，∴EF=2，OE=
| 3 |
在等腰Rt△PEF中，∠PEF=45°．∴PE=PF=
| 2 |
在Rt△OPF中，sin∠OPF=
| OF |
| PF |
| 1 | ||
|
| ||
| 2 |
∴二面角α---l---β的平面角为45°．
故选A．
点评：熟练掌握线面垂直的判定和性质定理、二面角的平面角的定义和作法是解题的关键．
练习册系列答案
相关题目
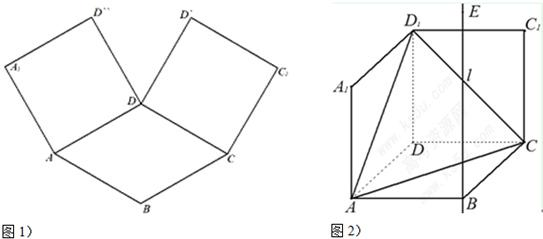
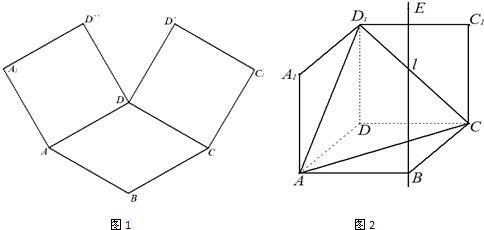
如图1，在平面内，ABCD是∠BAD=60°，且AB=a的菱形，ADD′′A1和CD D′C1都是正方形．将两个正方形分别沿AD，CD折起，使D′′与D′重合于点D1．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．
