题目内容
15.已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},0≤x<2}\\{lo{g}_{16}x,x≥2}\end{array}\right.$,若关于x的方程[f(x)]2+a•f(x)-a-1=0(a∈R)有且只有7个不同实数根,则a的取值范围是(-2,-$\frac{5}{4}$).分析 根据偶函数图象的对称性及指数函数、对数函数的单调性,由条件便可得出f(x)在(-∞,-2]和[0,2)上是减函数,在(-2,0]和[2,+∞)上是增函数,从而得到x=0时,f(x)取极大值1,x=±2时,f(x)取得极小值$\frac{1}{4}$,这样即可画出f(x)的草图,而解[f(x)]2+af(x)-a-1=0可得f(x)=1或f(x)=-a-1,从而便有$\frac{1}{4}<-a-1<1$,从而便可得出a的取值范围.
解答 解:由题意,f(x)在(-∞,-2]和[0,2)上是减函数,在(-2,0]和[2,+∞)上是增函数;
∴x=0时,函数取极大值1,x=±2时,取极小值$\frac{1}{4}$,且|x|≥16时,f(x)≥1,则f(x)的图象如下所示: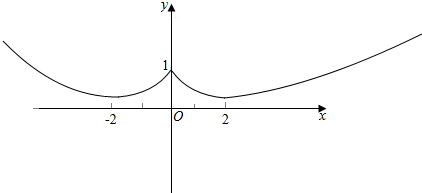
由[f(x)]2+a•f(x)-a-1=0得[f(x)-1][f(x)+a+1]=0;
∴f(x)=1或-a-1;
∵关于x的方程[f(x)]2+a•f(x)-a-1=0有7个不同实数根;
∴$\frac{1}{4}<-a-1<1$;
∴$-2<a<-\frac{5}{4}$;
∴a的取值范围为$(-2,-\frac{5}{4})$.
故答案为:$(-2,-\frac{5}{4})$.
点评 考查偶函数的定义,偶函数图象的对称性,以及指数函数和对数函数的单调性,以及函数极值的概念,一元二次方程的解法,数形结合解题的方法.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.已知函数$f(g(x))=sin2x,g(x)=tan({x+\frac{π}{4}})$,则$f(-\frac{1}{7})$=( )
| A. | $\frac{4}{3}$ | B. | $-\frac{4}{3}$ | C. | $-\frac{24}{25}$ | D. | $-\frac{24}{7}$ |
10.已知x=lnπ,y=log${\;}_{\frac{1}{2}}$π,z=e-2,则( )
| A. | x<y<z | B. | y<x<z | C. | y<z<x | D. | z<y<x |
20.从5名学生中选2名学生参加周日社会实验活动,学生甲被选中而学生乙没有被选中的方法种数是( )
| A. | 10 | B. | 6 | C. | 4 | D. | 3 |