题目内容
(本小题满分13分)
如图,矩形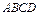 所在的平面与平面
所在的平面与平面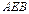 垂直,且
垂直,且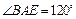 ,
,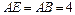 ,
,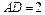 ,
,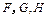 分别为
分别为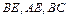 的中点.
的中点.

(Ⅰ) 求证:直线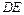 与平面
与平面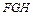 平行;
平行;
(Ⅱ)若点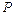 在直线
在直线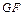 上,且二面角
上,且二面角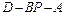 的大小为
的大小为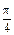 ,试确定点
,试确定点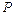 的位置.
的位置.
如图,矩形
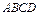 所在的平面与平面
所在的平面与平面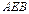 垂直,且
垂直,且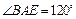 ,
,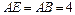 ,
,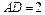 ,
,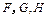 分别为
分别为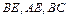 的中点.
的中点.
(Ⅰ) 求证:直线
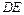 与平面
与平面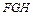 平行;
平行;(Ⅱ)若点
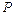 在直线
在直线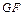 上,且二面角
上,且二面角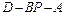 的大小为
的大小为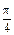 ,试确定点
,试确定点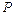 的位置.
的位置.(Ⅰ)证明:取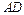 的中点
的中点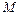 ,连结
,连结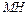 ,
,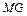 .
.

∵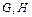 分别是
分别是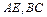 的中点,
的中点,
∴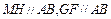 ,
,
∴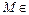 平面
平面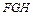 ,…………………3分
,…………………3分
又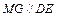 ,
,
且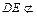 平面
平面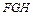 ,
,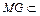 平面
平面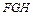 ,
,
∴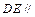 平面
平面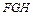 .…………………6分
.…………………6分
(Ⅱ)解:如图,在平面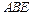 内,过
内,过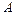 作
作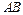 的垂线,记为
的垂线,记为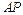 ,则
,则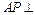 平面
平面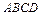 .
.
以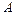 为原点,
为原点,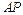 、
、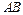 、
、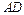 所在的直线分别为
所在的直线分别为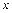 轴,
轴,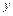 轴,
轴,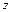 轴建立建立空间直角坐标系
轴建立建立空间直角坐标系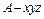 .
.
∴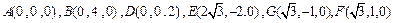 .
.
∴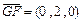 ,
,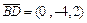 ,
,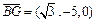 . …………………8分
. …………………8分
设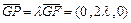 ,则
,则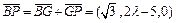 .
.
设平面 的法向量为
的法向量为 ,
,
则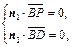 ∴
∴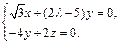
取 ,得
,得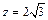 ,
,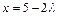 ,
,
∴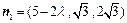 .
.
又平面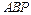 的法向量为
的法向量为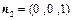 , .…………………11分
, .…………………11分
∴ ,
,
解得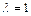 或
或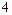 .
.
故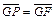 或
或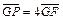 (
(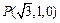 或
或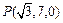 ). …………………13分
). …………………13分
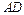 的中点
的中点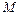 ,连结
,连结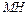 ,
,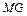 .
.
∵
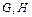 分别是
分别是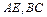 的中点,
的中点,∴
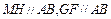 ,
,∴
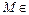 平面
平面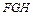 ,…………………3分
,…………………3分又
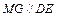 ,
,且
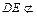 平面
平面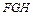 ,
,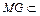 平面
平面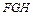 ,
,∴
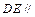 平面
平面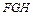 .…………………6分
.…………………6分(Ⅱ)解:如图,在平面
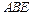 内,过
内,过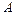 作
作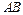 的垂线,记为
的垂线,记为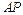 ,则
,则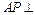 平面
平面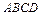 .
. 以
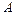 为原点,
为原点,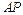 、
、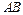 、
、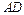 所在的直线分别为
所在的直线分别为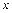 轴,
轴,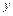 轴,
轴,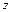 轴建立建立空间直角坐标系
轴建立建立空间直角坐标系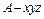 .
. ∴
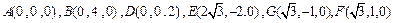 .
.∴
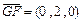 ,
,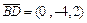 ,
,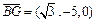 . …………………8分
. …………………8分设
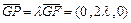 ,则
,则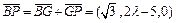 .
. 设平面
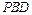 的法向量为
的法向量为 ,
,则
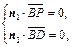 ∴
∴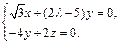
取
 ,得
,得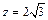 ,
,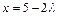 ,
,∴
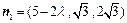 .
. 又平面
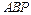 的法向量为
的法向量为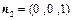 , .…………………11分
, .…………………11分∴
 ,
,
解得
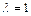 或
或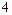 .
. 故
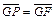 或
或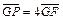 (
(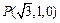 或
或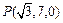 ). …………………13分
). …………………13分略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
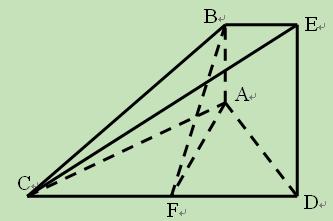
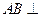 平面
平面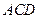 ,
,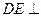 平面
平面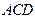 ,△
,△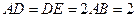 ,
,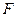 为
为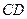 的中点.
的中点.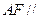 平面
平面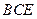 ;
;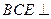 平面
平面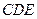 。
。

 的正方体
的正方体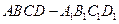 中,
中,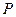 为线段
为线段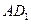 上的点,且满足
上的点,且满足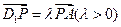 .
.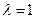 时,求证:平面
时,求证:平面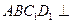 平面
平面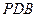 ;
;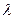 为何值,三棱锥
为何值,三棱锥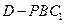 的体积
的体积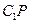 与
与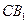 所成的角的余弦值.
所成的角的余弦值.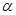 ,
,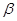 ,
,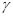 两两互相垂直,点
两两互相垂直,点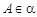 ,点
,点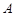 到
到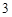 ,点
,点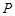 是
是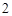 倍,则点
倍,则点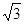
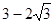
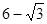
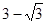
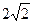 .
.
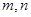 为直线,
为直线,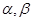 为平面,给出下列命题:
为平面,给出下列命题: ②
②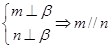 ③
③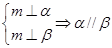 ④
④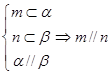
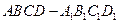 中,异面直线
中,异面直线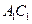 与
与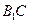 的夹角的大小为__________
的夹角的大小为__________