题目内容
已知函数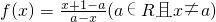 .
.
(1)求证:f(x)+f(2a-x)+2=0对定义域内的所有x都成立;
(2)当f(x)的定义域为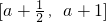 时,求证:f(x)的值域为[-3,-2].
时,求证:f(x)的值域为[-3,-2].
证明:(1)∵f(x)=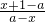 =
= -1,
-1,
∴f(2a-x)= -1=-
-1=- -1,
-1,
∴f(x)+f(2a-x)+2= +(-
+(- )-2+2=0,与x取值无关.
)-2+2=0,与x取值无关.
∴f(x)+f(2a-x)+2=0对定义域内的所有x都成立;
(2)∵f(x)的定义域为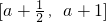 ,
,
∴-1-a≤-x≤-a- ,-1≤a-x≤-
,-1≤a-x≤- ,-2≤
,-2≤ ≤-1,
≤-1,
又f(x)= -1,
-1,
∴-3≤ -1≤-2,即f(x)的值域为[-3,-2].
-1≤-2,即f(x)的值域为[-3,-2].
分析:(1)由于f(x)= -1,于是可得f(x)+f(2a-x)+2=0,与x取值无关得证;
-1,于是可得f(x)+f(2a-x)+2=0,与x取值无关得证;
(2)由定义域为[a+12,a+1],得 ,再由f(x)=
,再由f(x)= -1即可求解.
-1即可求解.
点评:本题考查函数的值域,关键在于对f(x)的化简(化为f(x)= -1),难点在于由x的范围到-x的范围,再到a-x的范围,最后到
-1),难点在于由x的范围到-x的范围,再到a-x的范围,最后到 的范围的探讨,属于难题.
的范围的探讨,属于难题.
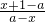 =
= -1,
-1,∴f(2a-x)=
 -1=-
-1=- -1,
-1,∴f(x)+f(2a-x)+2=
 +(-
+(- )-2+2=0,与x取值无关.
)-2+2=0,与x取值无关.∴f(x)+f(2a-x)+2=0对定义域内的所有x都成立;
(2)∵f(x)的定义域为
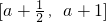 ,
,∴-1-a≤-x≤-a-
 ,-1≤a-x≤-
,-1≤a-x≤- ,-2≤
,-2≤ ≤-1,
≤-1,又f(x)=
 -1,
-1,∴-3≤
 -1≤-2,即f(x)的值域为[-3,-2].
-1≤-2,即f(x)的值域为[-3,-2].分析:(1)由于f(x)=
 -1,于是可得f(x)+f(2a-x)+2=0,与x取值无关得证;
-1,于是可得f(x)+f(2a-x)+2=0,与x取值无关得证;(2)由定义域为[a+12,a+1],得
 ,再由f(x)=
,再由f(x)= -1即可求解.
-1即可求解.点评:本题考查函数的值域,关键在于对f(x)的化简(化为f(x)=
 -1),难点在于由x的范围到-x的范围,再到a-x的范围,最后到
-1),难点在于由x的范围到-x的范围,再到a-x的范围,最后到 的范围的探讨,属于难题.
的范围的探讨,属于难题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





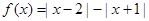 .
. ;
;
 .
. ;
; .
. .
. 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
) 时,若关于
时,若关于 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围. .
. 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
) 时,若关于
时,若关于 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.