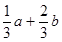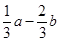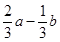题目内容
设函数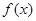 的定义域为
的定义域为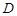 ,如果对于任意
,如果对于任意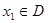 ,存在唯一
,存在唯一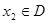 ,使
,使
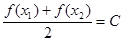 (
(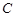 为常数)成立,则称
为常数)成立,则称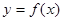 在
在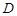 上的均值为
上的均值为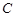 ,给出下列四个
,给出下列四个
函数: ①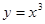 ;②
;②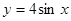 ;③
;③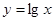 ;④
;④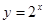 . 则满足在其定义域上均值为2
. 则满足在其定义域上均值为2
的所有函数是__________.
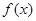 的定义域为
的定义域为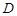 ,如果对于任意
,如果对于任意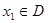 ,存在唯一
,存在唯一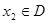 ,使
,使 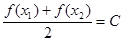 (
(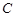 为常数)成立,则称
为常数)成立,则称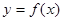 在
在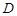 上的均值为
上的均值为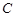 ,给出下列四个
,给出下列四个函数: ①
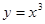 ;②
;②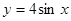 ;③
;③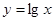 ;④
;④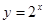 . 则满足在其定义域上均值为2
. 则满足在其定义域上均值为2的所有函数是__________.
(1),(3)
解:因为首先分析题目求对于任意的x1∈D,存在唯一的x2∈D,使
=2对于函数①y=x3,可直接取任意的x1∈R,验证求出唯一的x2=  ,即可得到成立.
,即可得到成立.
对于函数②y=4sinx,因为y=4sinx是R上的周期函数,明显不成立.对于函数③y=lgx,定义域为x>0,值域为R且单调,显然成立.
对于函数④y=2x,特殊值法代入验证不成立成立.即可得到答案
| f(x1)+f(x2) |
| 2 |
 ,即可得到成立.
,即可得到成立.对于函数②y=4sinx,因为y=4sinx是R上的周期函数,明显不成立.对于函数③y=lgx,定义域为x>0,值域为R且单调,显然成立.
对于函数④y=2x,特殊值法代入验证不成立成立.即可得到答案

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
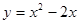 ,
,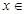 [0,3]的值域是
[0,3]的值域是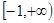
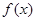 称为“好函数”:对于在
称为“好函数”:对于在 ,若这三个数能作为三角形的三边长,则
,若这三个数能作为三角形的三边长,则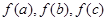 也能作为三角形的三边长.现有如下一些函数:
也能作为三角形的三边长.现有如下一些函数: 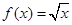 ②
②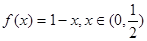
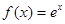 ,
, ④
④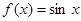 ,
,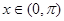 .
.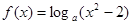 , 若
, 若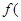 2)=1,求
2)=1,求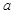 的值;
的值;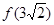 的值;
的值;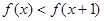 的解集.
的解集. CPD的面积为
CPD的面积为 ,则
,则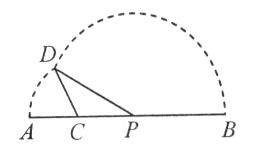
 :当
:当 时,
时, ;当
;当 时,
时,  ,则函数
,则函数 ,
,  的最大值等于( )
的最大值等于( )
 成立,求实数a的取值范围;
成立,求实数a的取值范围; 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.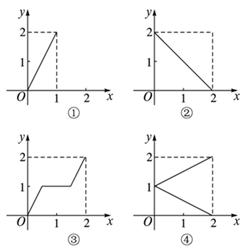
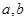 的代数式为
的代数式为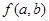 ,它满足关系:
,它满足关系: ; ②
; ②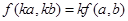 ;
; 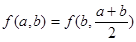 ;④
;④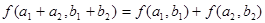 ,
,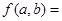 ( )
( )