题目内容
函数f(x)=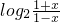 (x≠0)的图象在
(x≠0)的图象在
- A.一、三象限
- B.二、四象限
- C.一、二象限
- D.三、四象限
A
分析:由题设知函数f(x)的定义域是(-1,1),f(-x)=lg =-lg
=-lg =-f(x),所以函数f(x)=lg
=-f(x),所以函数f(x)=lg 是奇函数,其图象关于原点对称.由此能够求出结果.
是奇函数,其图象关于原点对称.由此能够求出结果.
解答:∵函数f(x)=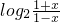 (x≠0),
(x≠0),
∴函数f(x)的定义域是(-1,1).
f(-x)=lg =-lg
=-lg =-f(x),
=-f(x),
∴函数f(x)=lg 是奇函数.
是奇函数.
∴函数f(x)=lg 的图象关于原点对称.
的图象关于原点对称.
∴函数f(x)=lg 的图象不可能在一、二象限,也不可能在三、四象限,
的图象不可能在一、二象限,也不可能在三、四象限,
故排除选项C和D,
∵0<x<1时, ,f(x)=lg
,f(x)=lg >0,
>0,
-1<x<0时, ,f(x)=lg
,f(x)=lg <0,
<0,
∴函数f(x)=lg (x≠0)的图象在一、三象限.
(x≠0)的图象在一、三象限.
故选A.
点评:本题考查对数函数的图象和性质,解题时要认真审题,仔细解答,注意奇函数性质的应用.
分析:由题设知函数f(x)的定义域是(-1,1),f(-x)=lg
 =-lg
=-lg =-f(x),所以函数f(x)=lg
=-f(x),所以函数f(x)=lg 是奇函数,其图象关于原点对称.由此能够求出结果.
是奇函数,其图象关于原点对称.由此能够求出结果.解答:∵函数f(x)=
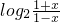 (x≠0),
(x≠0),∴函数f(x)的定义域是(-1,1).
f(-x)=lg
 =-lg
=-lg =-f(x),
=-f(x),∴函数f(x)=lg
 是奇函数.
是奇函数.∴函数f(x)=lg
 的图象关于原点对称.
的图象关于原点对称.∴函数f(x)=lg
 的图象不可能在一、二象限,也不可能在三、四象限,
的图象不可能在一、二象限,也不可能在三、四象限,故排除选项C和D,
∵0<x<1时,
 ,f(x)=lg
,f(x)=lg >0,
>0,-1<x<0时,
 ,f(x)=lg
,f(x)=lg <0,
<0,∴函数f(x)=lg
 (x≠0)的图象在一、三象限.
(x≠0)的图象在一、三象限.故选A.
点评:本题考查对数函数的图象和性质,解题时要认真审题,仔细解答,注意奇函数性质的应用.

练习册系列答案
相关题目