题目内容
已知两函数f(x)=8x2+16x-m,g(x)=2x3+5x2+4x,(m∈R)若对?x1∈[-3,3],?x2∈[-3,3],恒有f(x1)>g(x2)成立,求m的取值范围.
分析:若对?x1∈[-3,3],?x2∈[-3,3],恒有f(x1)>g(x2)成立,只需在∈[-3,3]上f(x)min>g(x)min即可.分别利用二次函数的图象与性质与导数求出两个最小值,列不等式求解即可.
解答:解:若对?x1∈[-3,3],?x2∈[-3,3],恒有f(x1)>g(x2)成立,只需在∈[-3,3]上f(x)min>g(x)min即可.
f(x)=8x2+16x-m=8(x+1)2-m-8,f(x)min=f(-1)=-m-8
g(x)=2x3+5x2+4x,g′(x)=6x2+10x+4=(x+1)(6x+4),
在x∈(-3,-1)∪(-
,3],g′(x)>0,(-3,-1)与(-
,3]是g(x)单调递增区间.在x∈(-1,-
),g′(x)<0,(-1,-
,]是g(x)单调递减区间.
g(x)的极小值为g(-
)=-
,又g(-3)=-21,所以g(x)min=-21
所以-m-8>-21,解得m的范围为m<13.
f(x)=8x2+16x-m=8(x+1)2-m-8,f(x)min=f(-1)=-m-8
g(x)=2x3+5x2+4x,g′(x)=6x2+10x+4=(x+1)(6x+4),
在x∈(-3,-1)∪(-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
g(x)的极小值为g(-
| 2 |
| 3 |
| 28 |
| 27 |
,又g(-3)=-21,所以g(x)min=-21
所以-m-8>-21,解得m的范围为m<13.
点评:本题考查函数的最值及应用,将问题转化为f(x)min>g(x)min是关键.考查逻辑推理、转化计算等能力.

练习册系列答案
相关题目
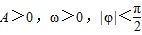 ,若函数f(x)的图象在y轴右侧的第一个最大值点和第一个最小值点分别为(π,2)和(4π,-2).
,若函数f(x)的图象在y轴右侧的第一个最大值点和第一个最小值点分别为(π,2)和(4π,-2).