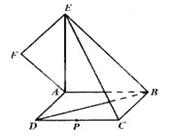
题目内容
(本题满分14分)如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4.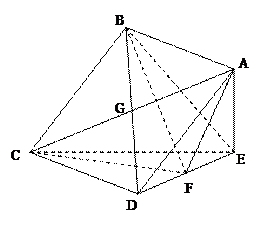
(Ⅰ)若F为DE的中点,求证:BE//平面ACF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值.
解:(Ⅰ)设AC与BD相交于G,连结GF.
正方形ABCD,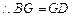 ,又
,又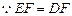 ,
, ,………………………………………2分
,………………………………………2分 平面ACF,
平面ACF, 平面ACF,
平面ACF,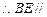 平面ACF………………………………3分
平面ACF………………………………3分
(Ⅱ)解法一:过E点作EH⊥AD,垂足为H,连结BH……….1分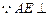 平面CDE,
平面CDE,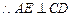 ,又
,又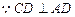 ,
, ,
,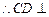 平面ADE,
平面ADE,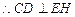 ,
,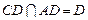 ,
,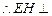 平面ABCD,
平面ABCD,
所以 是直线BE与平面ABCD所成的角…………………….4分
是直线BE与平面ABCD所成的角…………………….4分
Rt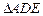 中,AE=3,DE=4,
中,AE=3,DE=4,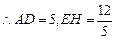 .
.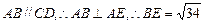 ,
, 所以直线BE与平面ABCD所成角的正弦值为
所以直线BE与平面ABCD所成角的正弦值为 ......4分
......4分
解法二: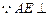 平面CDE,
平面CDE,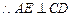 ,又
,又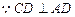 ,
, ,
,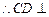 平面ADE,
平面ADE, 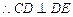 ,
,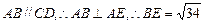 ,........4分
,........4分
Rt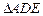 中,AE=3,DE=4,
中,AE=3,DE=4,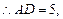
 ,即
,即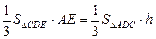 ,
,
设直线BE与平面ABCD所成角为 ,
,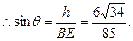
所以直线BE与平面ABCD所成角的正弦值为
解析

练习册系列答案
相关题目
在空间直角坐标系中,点A(1,﹣1,1)与点B(﹣1,﹣1,﹣1)关于( )对称
| A.x轴 | B.y轴 | C.z轴 | D.原点 |
 中.
中. 与
与 所成角的大小;
所成角的大小; 的正切值.
的正切值.
 中,底面
中,底面 是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
 的三视图如图所示,
的三视图如图所示, 其中正视图
其中正视图 和侧视图
和侧视图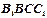 均为矩形,俯视图
均为矩形,俯视图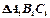 中,
中,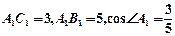 。
。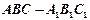 中,求证:
中,求证: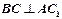 ;
;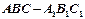 中,若
中,若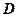 是底边
是底边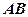 的中点,求证:
的中点,求证: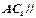 平面
平面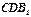 ;
;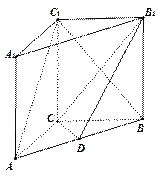
 。
。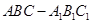 的底面
的底面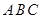 位于平行四边形
位于平行四边形 中,
中,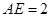 ,
,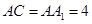 ,
, ,点
,点 为
为 中点.
中点.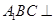 平面
平面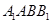 .
.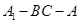 的大小为
的大小为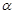 ,直线
,直线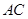 与平面
与平面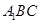 所成的角为
所成的角为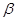 ,求
,求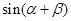 的值.
的值.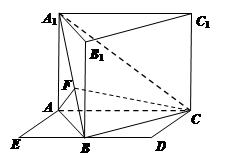
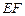 ⊥平面
⊥平面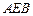 ,
, 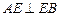 ,
,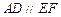 ,
,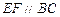 ,
,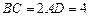 ,
,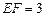 ,
,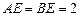 ,
,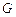 是
是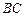 的中点.
的中点.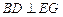 ;
;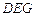 与平面
与平面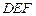 所成锐二面角的余弦值.
所成锐二面角的余弦值.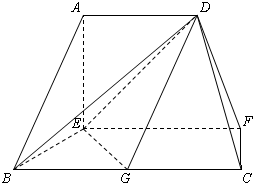

 ∠AEF=45°
∠AEF=45°