题目内容
（2012•包头一模）如图，A，B，C，D四点在同一圆上，BC与AD的延长线交于点E，点F在BA的延长线上．（Ⅰ）若
| EC |
| EB |
| 1 |
| 3 |
| ED |
| EA |
| 1 |
| 2 |
| DC |
| AB |
（Ⅱ）若EF2=FA•FB，证明：EF∥CD．
分析：（I）根据圆内接四边形的性质，可得∠ECD=∠EAB，∠EDC=∠B，从而△EDC∽△EBA，所以有
=
=
，利用比例的性质可得
•
=(
)2，得到
=
；
（II）根据题意中的比例中项，可得
=
，结合公共角可得△FAE∽△FEB，所以∠FEA=∠EBF，再由（I）的结论∠EDC=∠EBF，利用等量代换可得∠FEA=∠EDC，内错角相等，所以EF∥CD．
| ED |
| EB |
| EC |
| EA |
| DC |
| AB |
| 1 |
| 2 |
| 1 |
| 3 |
| DC |
| AB |
| DC |
| AB |
| ||
| 6 |
（II）根据题意中的比例中项，可得
| EF |
| FA |
| FB |
| FE |
解答：解：（Ⅰ）∵A，B，C，D四点共圆，
∴∠ECD=∠EAB，∠EDC=∠B
∴△EDC∽△EBA，可得
=
=
，
∴
•
=(
)2，即
•
=(
)2
∴
=
（Ⅱ）∵EF2=FA•FB，
∴
=
，
又∵∠EFA=∠BFE，
∴△FAE∽△FEB，可得∠FEA=∠EBF，
又∵A，B，C，D四点共圆，
∴∠EDC=∠EBF，
∴∠FEA=∠EDC，
∴EF∥CD．
∴∠ECD=∠EAB，∠EDC=∠B
∴△EDC∽△EBA，可得
| ED |
| EB |
| EC |
| EA |
| DC |
| AB |
∴
| ED |
| EB |
| EC |
| EA |
| DC |
| AB |
| 1 |
| 2 |
| 1 |
| 3 |
| DC |
| AB |
∴
| DC |
| AB |
| ||
| 6 |
（Ⅱ）∵EF2=FA•FB，
∴
| EF |
| FA |
| FB |
| FE |
又∵∠EFA=∠BFE，
∴△FAE∽△FEB，可得∠FEA=∠EBF，
又∵A，B，C，D四点共圆，
∴∠EDC=∠EBF，
∴∠FEA=∠EDC，
∴EF∥CD．
点评：本题在圆内接四边形的条件下，一方面证明两条直线平行，另一方面求线段的比值．着重考查了圆中的比例线段、圆内接四边形的性质和相似三角形的判定与性质等知识点，属于中档题．
练习册系列答案
相关题目
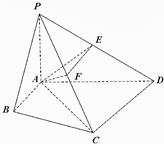（2012•包头一模）在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2，AB=1．
（2012•包头一模）函数f（x）=sin（ωx+?）（其中