题目内容
设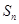 为数列
为数列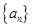 的前
的前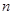 项和,对任意的
项和,对任意的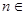 N,都有
N,都有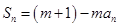
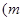 为常数,且
为常数,且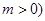 .
.
(1)求证:数列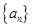 是等比数列;
是等比数列;
(2)设数列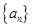 的公比
的公比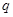 与
与 函数关系为
函数关系为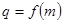 ,数列
,数列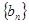 满足
满足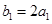 ,点
,点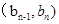 落在
落在 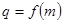 上,
上,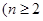 ,
,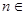 N,求数列
N,求数列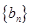 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列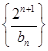 的前
的前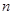 项和
项和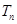 ,使
,使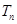
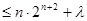 恒成立时,求
恒成立时,求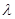 的最小值.[
的最小值.[
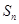 为数列
为数列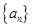 的前
的前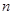 项和,对任意的
项和,对任意的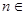 N,都有
N,都有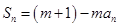
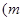 为常数,且
为常数,且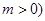 .
.(1)求证:数列
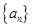 是等比数列;
是等比数列;(2)设数列
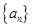 的公比
的公比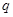 与
与 函数关系为
函数关系为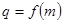 ,数列
,数列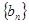 满足
满足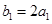 ,点
,点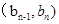 落在
落在 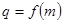 上,
上,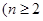 ,
,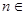 N,求数列
N,求数列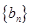 的通项公式;
的通项公式;(3)在满足(2)的条件下,求数列
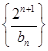 的前
的前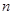 项和
项和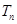 ,使
,使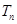
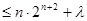 恒成立时,求
恒成立时,求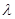 的最小值.[
的最小值.[(1)证明过程详见试题分析; (2)数列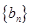 的通项公式为
的通项公式为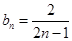 ;
;
(3)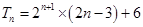 ,
,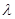 的最小值为-6.
的最小值为-6.
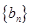 的通项公式为
的通项公式为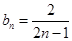 ;
;(3)
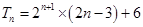 ,
,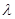 的最小值为-6.
的最小值为-6.试题分析:(1)按照等比数列的定义证明数列
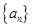 是等比数列;
是等比数列;(2)由(1)知
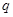 与
与 函数关系为
函数关系为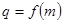
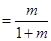 ,∴
,∴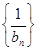 是首项为
是首项为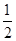 ,公差为1的等差数列,通项公式可求;
,公差为1的等差数列,通项公式可求;(3)先用错位相减法求出数列
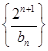 的前
的前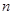 项和
项和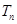 ,即
,即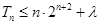 ,化简得
,化简得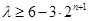 恒成立,由单调性知当
恒成立,由单调性知当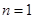 时,右边最大,所以
时,右边最大,所以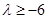 ,
,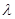 的最小值为-6.
的最小值为-6.(1)证明:当
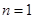 时,
时,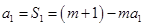 ,解得
,解得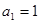 . 1分
. 1分当
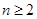 时,
时,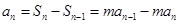 . 2分
. 2分即
 .
.∵
 为常数,且
为常数,且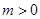 ,∴
,∴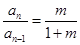
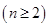 . 3分
. 3分∴数列
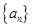 是首项为1,公比为
是首项为1,公比为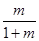 的等比数列. 4分
的等比数列. 4分(2)解:由(1)得,
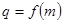
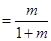 ,
,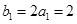 . 5分
. 5分∵
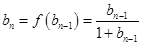
∴
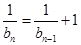 ,即
,即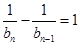
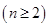 .
.∴
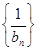 是首项为
是首项为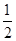 ,公差为1的等差数列. 7分
,公差为1的等差数列. 7分∴
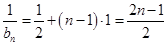 ,即
,即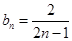 (
(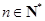 ). 8分
). 8分(3)解:由(2)知
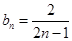 ,则
,则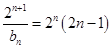 . 9分
. 9分所以
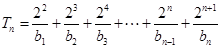 ,
,即
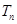
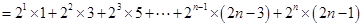 , ①
, ①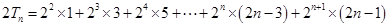 , ②
, ②②-①得
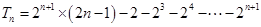 ,
, 故
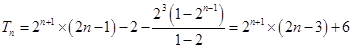 .
.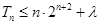 ,化简得
,化简得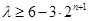 恒成立,由单调性知当
恒成立,由单调性知当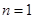 时,右边最大,所以
时,右边最大,所以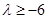 ,
,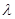 的最小值为-6. 14分
的最小值为-6. 14分
练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
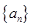 满足
满足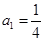 ,
,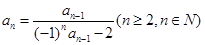 .
.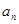 ;
;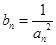 ,求数列
,求数列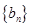 的前n项和
的前n项和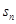 ;
;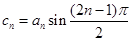 ,数列
,数列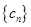 的前n项和为
的前n项和为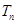 .求证:对任意的
.求证:对任意的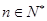 ,
,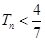 .
.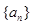 中,若
中,若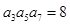 ,则
,则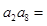 ( )
( )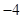
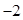
 。
。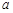 m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.
m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.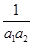 +
+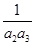 +…+
+…+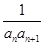 的结果可化为( )
的结果可化为( )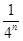
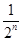
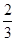 (1-
(1- 满足
满足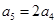 ,
,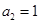 ,数列
,数列 项和
项和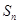 ,则
,则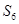 = .
= .