题目内容
在数列{ }中,
}中, ,
, ,设
,设 ,
,
(1)证明:数列{ }是等差数列;
}是等差数列;
(2)求数列{ }的前n项和
}的前n项和 ;
;
(3)设 ,证明:
,证明:
 }中,
}中, ,
, ,设
,设 ,
,(1)证明:数列{
 }是等差数列;
}是等差数列;(2)求数列{
 }的前n项和
}的前n项和 ;
;(3)设
 ,证明:
,证明:
(1)证明如下(2)
(3)

(3)

试题分析:(1)证明:由
 得:
得:
又因为
 ,所以
,所以
所以数列{
 }是等差数列
}是等差数列(2)数列{
 }的首项是:
}的首项是: ,
,又因为公差
 ,所以
,所以
由
 得:
得:
所以数列{
 }的前n项和
}的前n项和
所以

两式相减得

所以

(3)因为
 ,所以
,所以
所以

点评:对于求一般数列的通项公式或前n项和时,常用方法有:错位相减法、裂变法等,目的是消去中间部分,本题在求前n项和
 时就用到裂变法。
时就用到裂变法。
练习册系列答案
相关题目
 中,
中, …
… ,公比
,公比 ,则
,则 …
… .
. 中,
中,  则
则 ( )
( ) 中,
中, ,
, 则数列的公比
则数列的公比 为 ( )
为 ( )



 的前n项和为
的前n项和为 ,
, ,且
,且 ,数列
,数列 满足
满足 ,数列
,数列 的前n项和为
的前n项和为 (其中
(其中 ).
). 和
和 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 ,
,
 中,若
中,若 ,
, ,则
,则 的值为( )
的值为( )



 的公比
的公比 ,且
,且 ,又
,又 ,那么( )
,那么( )


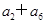 与
与 的大小不能确定
的大小不能确定