题目内容
方程x2+y2+2ax-by+c=0表示圆心为C（2，2），半径为2的圆，则a，b，c的值依次为（ ）
| A、2，4，4 | B、-2，4，4 | C、2，-4，4 | D、2，-4，-4 |
分析：先根据方程求出用a、b和c表示的圆心坐标和圆的半径，再由题意代入对应的式子求出a、b和c的值．
解答：解：由x2+y2+2ax-by+c=0得，圆心坐标是（-a，
），半径为r2=
+a2-c，
因圆心为C（2，2），半径为2，解得a=-2，b=4，c=4，
故选B．
| b |
| 2 |
| b2 |
| 4 |
因圆心为C（2，2），半径为2，解得a=-2，b=4，c=4，
故选B．
点评：本题考查了二元二次方程表示圆的问题，即根据方程表示出圆心坐标以及半径，再把条件代入进行求值．
练习册系列答案
名校课堂系列答案
相关题目
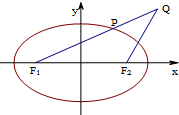已知椭圆