Question

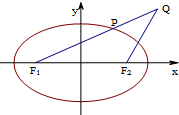已知椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的左右焦点为F₁（-c，0），F₂（c，0），点Q是椭圆外的动点，满足|

F1Q

|=2a，点P是线段F₁Q与该椭圆的交点，曲线C的方程是x²+y²=a²
（1）若点P的横坐标为

a

2

，证明：|

F1P

|=a+

c

2

（2）试问：曲线C上是否存在点M，使得△F₁MF₂的面积等于S=b²？若存在，求出椭圆离心率的取值范围；若不存在，请说明理由．

Answer 1

分析：（1）确定椭圆的左准线方程，利用椭圆的定义，可得

| F1P |

| a 2 + a2 c |

=

c

a

，从而可得结论；
（2）利用存在点M，使得△F₁MF₂的面积等于b²，确定M的纵坐标，即可求椭圆离心率的取值范围．

解答：（1）证明：椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的左准线方程为x=-

a2

c

∵点P的横坐标为

a

2

，
∴由椭圆的定义可知，

| F1P |

| a 2 + a2 c |

=

c

a

，
∴|

F1P

|=a+

c

2

；
（2）解：假设存在，设M（x，y），则
∵△F₁MF₂的面积等于S=b²，
∴

1

2

•2c•|y|=b2
∴|y|=

b2

c

∵M在x²+y²=a²上，
∴

b2

c

≤a
∴e²+e-1≥0
∴e≥

2

-

1

2

或e≤-

2

-

1

2

∵0＜e＜1
∴

2

-

1

2

≤e＜1．

点评：本题考查椭圆的定义，考查椭圆的性质，考查学生分析解决问题的能力，属于中档题．