题目内容
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为![]() .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为![]() .
.
(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;
(Ⅱ)求![]() 的值;
的值;
(Ⅲ)设甲、乙、丙三人中破译出密码的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
解:记“甲、乙、丙三人各自破译出密码”分别为事件![]() ,依题意有
,依题意有
![]() 且
且![]() 相互独立.
相互独立.
(Ⅰ)甲、乙二人中至少有一人破译出密码的概率为
![]()
![]() . …………………3分
. …………………3分
(Ⅱ)设“三人中只有甲破译出密码”为事件![]() ,则有
,则有
![]()
![]() =
=![]() , …………………5分
, …………………5分
所以![]() ,
,![]() . ……………………7分
. ……………………7分
(Ⅲ)![]() 的所有可能取值为
的所有可能取值为![]() . ……………………8分
. ……………………8分
所以![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() =
=![]()
![]() =
=![]() . ……………………11分
. ……………………11分
![]() 分布列为:
分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
……………………12分
所以,![]() . ……………………13分
. ……………………13分

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
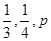 ,
,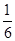 .
.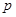 的值,
的值,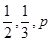 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为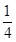 .
.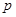 的值;
的值;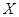 ,求
,求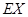 .
.