题目内容
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为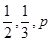 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为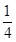 .
.
(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;
(Ⅱ)求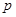 的值;
的值;
(Ⅲ)设甲、乙、丙三人中破译出密码的人数为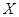 ,求
,求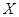 的分布列和数学期望
的分布列和数学期望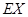 .
.
【答案】
(1)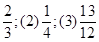 .
.
【解析】(2)可以利用对立事件来做:那就是先求出甲乙二人都没有破译出密码的概率,然后利用相互对立事件的概率和为1求解.
(2)根据三人中只有甲破译出密码的概率为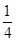 ,可求出丙独自破译出密码的概率p.
,可求出丙独自破译出密码的概率p.
(3)X的可能值不能搞错:有0,1,2,3.然后分别求出其概率,求出分布列,再利用期望公式求解即可.
解:记“甲、乙、丙三人各自破译出密码”分别为事件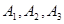 ,依题意有
,依题意有
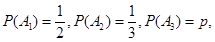 且
且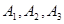 相互独立.
相互独立.
(Ⅰ)甲、乙二人中至少有一人破译出密码的概率为 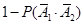
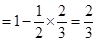 .
.
(Ⅱ)设“三人中只有甲破译出密码”为事件 ,则有
,则有
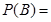
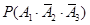 =
=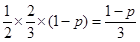 , 所以
, 所以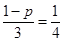 ,
,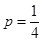 .
.
(Ⅲ)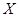 的所有可能取值为
的所有可能取值为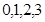 . 所以
. 所以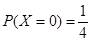 ,
,
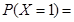
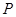
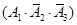
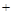
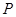
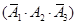
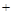
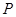
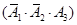
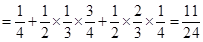 ,
,
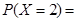
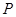
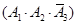
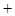
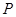
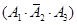
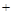
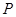
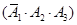
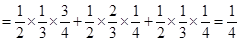 ,
,
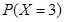 =
=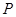
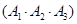 =
=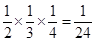 .
.
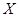 分布列为:
分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
所以,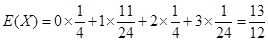 .
.

练习册系列答案
相关题目






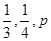 ,
,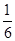 .
.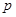 的值,
的值,