题目内容
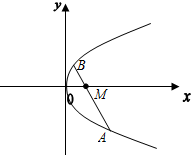 如图,M(a,0)(a>0)是抛物线y2=4x对称轴上一点,过M作抛物线的弦AMB,交抛物线与A,B.
如图,M(a,0)(a>0)是抛物线y2=4x对称轴上一点,过M作抛物线的弦AMB,交抛物线与A,B.(1)若a=2,求弦AB中点的轨迹方程;
(2)若AB=8,求a的取值范围.
分析:(1)分两种情况进行讨论:当AB斜率存在时,由a=2,设其方程为y=k(x-2),弦AB中点为(x0,y0),联立直线与抛物线方程消掉y得x的二次方程,由韦达定理及中点坐标公式可用k表示x0,y0,消掉k可得轨迹方程;当AB斜率不存在时,易求弦中点坐标代入上述方程检验即可;
(2)当AB斜率不存在时,由AB=8易求a值;当AB斜率存在时,设其方程为y=k(x-a),代入抛物线方程得k2x2-(2ak2+4)x+a2k2=0,△>0,由弦长公式可用k表示出弦长,由题意知关于k的方程|AB|=8的方程有解,换元后转化为二次方程有正根,利用二次方程根的分布可得不等式,解出即可;
(2)当AB斜率不存在时,由AB=8易求a值;当AB斜率存在时,设其方程为y=k(x-a),代入抛物线方程得k2x2-(2ak2+4)x+a2k2=0,△>0,由弦长公式可用k表示出弦长,由题意知关于k的方程|AB|=8的方程有解,换元后转化为二次方程有正根,利用二次方程根的分布可得不等式,解出即可;
解答:解:(1)当AB斜率存在时,由a=2,设其方程为y=k(x-2),弦AB中点为(x0,y0),
由
得k2x2-4(k2+1)x+4k2=0,
△=16(k2+1)2-16k4=32k2+16>0,则
,
消去k得y02=2x0-4(x0>2);
当AB斜率不存在时,其方程为x=2,与抛物线相交,中点为(2,0),满足y2=2x-4.
综上所述,弦AB中点的轨迹方程y2=2x-4.
(2)当AB斜率不存在时,由AB=8,及抛物线的对称性知,A点的纵坐标为-4,则横坐标为4,故此时a=4; 7′
当AB斜率存在时,设其方程为y=k(x-a),代入抛物线方程得k2x2-(2ak2+4)x+a2k2=0,
△=4(ak2+2)2-4a2k4=16ak2+16>0,
,
|AB|=
=
,
则
=8有解,即方程(4-a)k4-(a+1)k2-1=0有解,
设t=k2(t>0),f(t)=(4-a)t2-(a+1)t-1=0 (1),
对于正数a,方程(1)一根为正一根为负的充要条件是
,得0<a<4;
对于正数a,方程(1)两根均为正的充要条件是
,即
,矛盾无解.
综上所述,a的取值范围是(0,4].
由
|
△=16(k2+1)2-16k4=32k2+16>0,则
|
消去k得y02=2x0-4(x0>2);
当AB斜率不存在时,其方程为x=2,与抛物线相交,中点为(2,0),满足y2=2x-4.
综上所述,弦AB中点的轨迹方程y2=2x-4.
(2)当AB斜率不存在时,由AB=8,及抛物线的对称性知,A点的纵坐标为-4,则横坐标为4,故此时a=4; 7′
当AB斜率存在时,设其方程为y=k(x-a),代入抛物线方程得k2x2-(2ak2+4)x+a2k2=0,
△=4(ak2+2)2-4a2k4=16ak2+16>0,
|
|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
4
| ||||
| k2 |
则
4
| ||||
| k2 |
设t=k2(t>0),f(t)=(4-a)t2-(a+1)t-1=0 (1),
对于正数a,方程(1)一根为正一根为负的充要条件是
|
对于正数a,方程(1)两根均为正的充要条件是
|
|
综上所述,a的取值范围是(0,4].
点评:本题考查直线与圆锥曲线的位置关系、轨迹方程的求解、弦长公式及二次方程根的分布问题,综合性强,运算量大.

练习册系列答案
相关题目
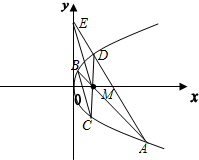 如图,M(a,0)(a>0)是抛物线y2=4x对称轴上一点,过M作抛物线的弦AMB,交抛物线与A,B.
如图,M(a,0)(a>0)是抛物线y2=4x对称轴上一点,过M作抛物线的弦AMB,交抛物线与A,B. (2012•温州一模)如图,过点A(0,-1)的动直线l与抛物线C:x2=4y交于P(x1,y1),Q(x2,y2)两点.
(2012•温州一模)如图,过点A(0,-1)的动直线l与抛物线C:x2=4y交于P(x1,y1),Q(x2,y2)两点. (1)若a=2,求弦AB中点的轨迹方程;
(1)若a=2,求弦AB中点的轨迹方程;