题目内容
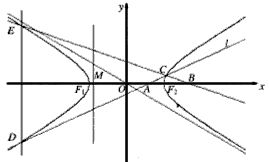
如图,双曲线![]() (a>0,b>0)的离心率为
(a>0,b>0)的离心率为![]() ,F1、F2分别为左、右焦点,
,F1、F2分别为左、右焦点,
M为左准线与渐近线在第二象限内的交点,且![]() .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)设A(m,0)和B(![]() ,0)(0<m<1)是x轴上的两点.过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.
,0)(0<m<1)是x轴上的两点.过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.
(Ⅰ)解:根据题设条件,F1(-c,0),F2(c,0).设点M(x,y).则x、y满足


因![]() ,解得
,解得![]() ,故
,故
![]()
=![]()
利用a2+b2=c2,得c2=![]() ,于是a2=1,b2=
,于是a2=1,b2=![]() .因此,所求双曲线方程为
.因此,所求双曲线方程为
x2-4y2=1.
(Ⅱ)解:设点C(x1,y1),D(x2,y2),E(x3,y3),则直线l的方程为
y=![]() (x-m).
(x-m).
于是C(x1,y1)、D(x2,y2)两点坐标满足

将(1)代入(2)得
(x12-2x1m+m2-4y12)x2+8my12x-4y12m2-x12+2mx1-m2=0.
由x21-4y21=1 (点C在双曲线上),上面方程可化简为
(m2-2x1m+1)x2+8my12x-(x12-2mx1+m2x12)=0.
由已知,显然m2-2x1m+1≠0.于是x1x2=-![]() .因为x1≠0,得
.因为x1≠0,得
x2=![]()
同理,C(x1,y1)、E(x3,y3)两点坐标满足

可解得
x3=
所以x2=x3,故直线DE垂直于x轴.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
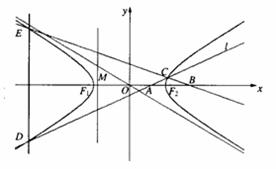
 如图,双曲线
如图,双曲线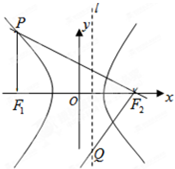 如图,F1(-c,0),F2(c,0)分别是双曲线C:
如图,F1(-c,0),F2(c,0)分别是双曲线C: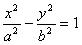 (a>0,b>0)的离心率为
(a>0,b>0)的离心率为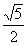 ,F1、F2分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且
,F1、F2分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且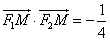 ,
,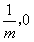 )(0<m<1)是x轴上的两点,过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E,证明直线DE垂直于x轴。
)(0<m<1)是x轴上的两点,过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E,证明直线DE垂直于x轴。