题目内容
11.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}x≤2\\|{y-2}|≤x\end{array}\right.$表示的平面区域的面积是( )| A. | $8\sqrt{2}$ | B. | 8 | C. | $4\sqrt{2}$ | D. | 4 |
分析 转化不等式为不等式组,画出约束条件表示的可行域,结合图形求解图形的面积.
解答 解:因为不等式|y-2|≤x≤2等价于$\left\{\begin{array}{l}{x≤2}\\{y-2≤x}\\{-x≤y-2}\end{array}\right.$,它的可行域为: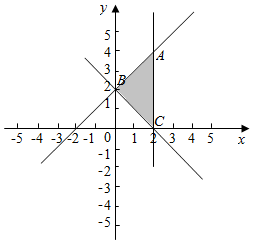
可行域是三角形,由 $\left\{\begin{array}{l}{x=2}\\{x=y-2}\end{array}\right.$得交点A(2,4),
C的坐标由 $\left\{\begin{array}{l}{x=2}\\{-x=y-2}\end{array}\right.$解得,为(2,0),B的坐标(0,2),
可行域三角形的面积为:$\frac{1}{2}$×4×2=4.
故选:D.
点评 本题考查线性规划,可行域的画法,思想的顶点坐标以及三角形的面积的求法,考查计算能力,转化思想的应用.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
1.一质点受到同一平面上的三个力F1,F2,F3(单位:牛顿)的作用而处于平衡状态.已知F1,F2成120°角,且F1,F2的大小分别为1和2,则F3的大小为( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
2.已知直线l的倾斜角为60°,则直线l的斜率为( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
19.等比数列{an}中,公比为3,且a2+a4=2,那么a3+a5的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
6.命题“任意x∈R,|x|≥0”的否定是( )
| A. | 任意x∈R,|x|<0 | B. | 任意x∈R,|x|≤0 | C. | 彐x∈R,|x|<0 | D. | 彐x∈R,|x|≤0 |
16.“(x+3)(x-1)=0”是“x-1=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |