题目内容
20.设0<x<1,则函数y=$\frac{1}{x}$+$\frac{1}{1-x}$的值域为[4,+∞).分析 由已知可得0<1-x<1,可得y=$\frac{1}{x}$+$\frac{1}{1-x}$=[x+(1-x)]($\frac{1}{x}$+$\frac{1}{1-x}$)=2+$\frac{1-x}{x}$+$\frac{x}{1-x}$,整体利用基本不等式可得.
解答 解:∵0<x<1,∴0<1-x<1,
∴y=$\frac{1}{x}$+$\frac{1}{1-x}$=[x+(1-x)]($\frac{1}{x}$+$\frac{1}{1-x}$)
=2+$\frac{1-x}{x}$+$\frac{x}{1-x}$≥2+2$\sqrt{\frac{1-x}{x}•\frac{x}{1-x}}$=4,
当且仅当$\frac{1-x}{x}$=$\frac{x}{1-x}$即x=$\frac{1}{2}$时取等号,
故函数y=$\frac{1}{x}$+$\frac{1}{1-x}$的值域为[4,+∞),
故答案为:[4,+∞).
点评 本题考查基本不等式求最值,整体凑出可用基本不等式的形式是解决问题的关键,属中档题.

练习册系列答案
相关题目
11.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}x≤2\\|{y-2}|≤x\end{array}\right.$表示的平面区域的面积是( )
| A. | $8\sqrt{2}$ | B. | 8 | C. | $4\sqrt{2}$ | D. | 4 |
9.将函数y=sin(2x-$\frac{π}{6}$)的图象向右平移$\frac{5π}{12}$个单位,得到g(x)的图象,则g(x)=( )
| A. | -sin2x | B. | sin2x | C. | -cos2x | D. | cos2x |
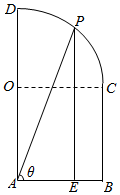 已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.
已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.