题目内容
1．二项式（1-2x）6展开式中x4的系数是240．分析 利用二项式展开式的通项公式，求出展开式中x的指数为4，从而求出对应的系数．
解答 解：二项式（1-2x）6展开式的通项公式为
Tr+1=${C}_{6}^{r}$•（-2x）r，
令r=4，
得T5=${C}_{6}^{4}$•（-2）4•x4=240x4，
所以该二项式展开式中x4的系数是240．
故答案为：240．
点评 本题考查了利用二项式展开式的通项公式求特定项的应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
11．在平面直角坐标系中，不等式组$\left\{\begin{array}{l}x≤2\\|{y-2}|≤x\end{array}\right.$表示的平面区域的面积是（ ）
| A． | $8\sqrt{2}$ | B． | 8 | C． | $4\sqrt{2}$ | D． | 4 |
9．将函数y=sin（2x-$\frac{π}{6}$）的图象向右平移$\frac{5π}{12}$个单位，得到g（x）的图象，则g（x）=（ ）
| A． | -sin2x | B． | sin2x | C． | -cos2x | D． | cos2x |
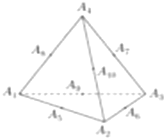已知正四面体A1A2A3A4，点A5，A6，A7，A8，A9，A10分别是所在棱的中点，如图，则当1≤i≤10，1≤j≤10，且i≠j时，数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9．